 |
ŚFiNiA
ŚFiNiA - Światopoglądowe, Filozoficzne, Naukowe i Artystyczne forum - bez cenzury, regulamin promuje racjonalną i rzeczową dyskusję i ułatwia ucinanie demagogii. Forum założone przez Wuja Zbója.
|
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 12:20, 21 Mar 2022 Temat postu: Wysłany: Pon 12:20, 21 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1550.html#652257
| Irbisol napisał: | | Oczywiście KRZ tego prawa nie uznaje? |
Prawo Słonia:
Matematycznie zachodzi tożsamość logiczna dla zbiorów:
1: Warunek wystarczający => <=> 2: relacja podzbioru => <=> 3: twierdzenie „Jeśli p to q” =>
Gdzie:
<=> - ten znaczek czytamy „wtedy i tylko wtedy”
„=”, <=> - tożsame znaczki tożsamości logicznej
KONIEC!
KRZ nie uznaje prawa Słonia, bo gdyby uznawało to musiałbyś dołożyć definicję implikacji rodem z KRZ.
W rzeczywistości jest tak:
Prawo Słonia:
Matematycznie zachodzi tożsamość logiczna dla zbiorów:
1: Warunek wystarczający => <=> 2: relacja podzbioru => <=> 3: twierdzenie „Jeśli p to q” =>
##
4: Implikacja rodem z KRZ =>
Gdzie:
## różne na mocy definicji
Poza tym nigdzie w Wikipedii nie znajdziesz prawa Słonia co oznacza, że KRZ tego prawa nie uznaje.
Gdyby ziemscy matematycy wiedzieli o prawie Słonia to prawo to byłoby w każdym podręczniku matematyki do LO bo prawo to fenomenalnie upraszcza dowody wszelkich twierdzeń matematycznych "Jeśli p to q".
cnd
Czekam kiedy zrozumiesz, że uznanie przez ziemskich matematyków prawa Słonia to Armagedon KRZ!
|
|
| Powrót do góry |
|
 |
|
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 13:52, 21 Mar 2022 Temat postu: Wysłany: Pon 13:52, 21 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1550.html#652281
| Irbisol napisał: | Wg KRZ jeżeli czegoś się nie stwierdza, to nie oznacza to stwierdzenia przeciwnego.
A u ciebie oznacza? |
Prawo Słonia:
Matematycznie zachodzi tożsamość logiczna dla zbiorów:
1: Warunek wystarczający => <=> 2: relacja podzbioru => <=> 3: twierdzenie „Jeśli p to q” =>
Gdzie:
<=> - ten znaczek czytamy „wtedy i tylko wtedy”
„=”, <=> - tożsame znaczki tożsamości logicznej
KONIEC!
ok
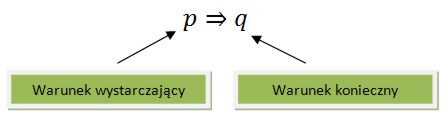
Zacznijmy po kolei od definicji warunku wystarczającego => :
2.
Definicja warunku wystarczającego => w zbiorach:
Jeśli p to q
p=>q =1
Zajście p jest (=1) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => jest (=1) spełniona wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Inaczej:
p=>q =0
Zajście p nie jest (=0) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => nie jest (=0) spełniona wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Czy powyższa definicja warunku wystarczającego => dla zbiorów znana jest w KRZ?
Jeśli tak, to proszę o zacytowanie jej z Wikipedii.
P.S.
Zauważ, że prawo Słonia obowiązuje tu na mocy definicji warunku wystarczającego =>
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 16:24, 21 Mar 2022 Temat postu: Wysłany: Pon 16:24, 21 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1550.html#652305
Dlaczego Irbisol kłamie?
2.
Definicja warunku wystarczającego => w zbiorach:
Jeśli p to q
p=>q =1
Zajście p jest (=1) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => jest (=1) spełniona wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Inaczej:
p=>q =0
Zajście p nie jest (=0) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => nie jest (=0) spełniona wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
| Irbisol napisał: |
Podawałem ci w angielskiej wikipedii |
Na 100% kłamiesz!
Oczywiście ponownego linku nie podasz, bo wszyscy zobaczyliby na własne oczy jak twój nosek … rośnie, rośnie, rośnie.
Dowód iż kłamiesz mamy w naszej polskiej Wikipedii:
[link widoczny dla zalogowanych]
| Wikpedia napisał: |
Warunek wystarczający
Warunek wystarczający (inaczej warunek dostateczny) – każdy warunek, z którego dany fakt wynika. Jeżeli warunek wystarczający zachodzi (wystarczy, by zachodził), wówczas zachodzi dany fakt.
Na przykład, jeżeli liczba jest podzielna przez 10, to jest podzielna przez 5. Fakt podzielności przez 10 jest warunkiem wystarczającym dla podzielności przez 5, natomiast fakt podzielności przez 5 jest warunkiem koniecznym dla podzielności przez 10.
Warunek wystarczający nie musi być warunkiem koniecznym — liczba nie musi wcale być podzielna przez 10, by była podzielna przez 5. |
Uważaj Irbisolu:
Gdyby ziemscy matematycy znali definicję warunku wystarczającego => jak na wstępie niniejszego postu, to przykład dla warunku wystarczającego => w Wikipedii byłby na 100% taki.
A1.
Jeśli dowolna liczba jest podzielna przez 10 to na 100% => jest podzielna przez 5
P10=>P5 =1
Podzielność dowolnej liczby przez 10 jest warunkiem wystarczającym => dla jej podzielności przez 5 wtedy i tylko wtedy gdy zbiór liczb podzielnych przez 10 P10=[10,20..] jest podzbiorem => zbioru liczb podzielnych przez 5 P5=[5,10,15,20..]
Wniosek:
Aby udowodnić prawdziwość warunku wystarczającego A1: P10=>P5 potrzeba i wystarcza udowodnić iż zbiór liczb podzielnych przez 10 P10=[10,20..] jest podzbiorem => zbioru liczb podzielnych przez 5 P5=[5,10,15,20..] … co udowodni każdy ziemski matematyk.
Zauważ Irbisolu, że definicja warunku wystarczającego => zapisana na wstępie podaje algorytm dowodu prawdziwości warunku wystarczającego => w zbiorach!
Na 100% nie ma tego algorytmu w gównie cytowanym w polskiej Wikipedii. ani też w jakiejkolwiek innej Wikipedii: Angielskiej, Chińskiej, czy Buszmeńskiej.
Irbisolu, choćbyś zjadł 1000 kotletów, to i tak w żadnej ziemskiej Wikipedii nie znajdziesz definicji warunku wystarczającego => jak na wstępie niniejszego postu, która zawiera algorytm dowodu prawdziwości warunku wystarczającego => w zbiorach.
Zauważ, że definicja warunku wystarczającego => ze wstępu niniejszego postu jest bajecznie prosta i zrozumiała dla ucznia I klasy LO oraz co najważniejsze - podaje algorytm dowodzenia prawdziwości warunku wystarczającego => w zbiorach!
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 17:41, 21 Mar 2022 Temat postu: Wysłany: Pon 17:41, 21 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1550.html#652319
| Irbisol napisał: | | Podajesz link do polskiej Wikipedii jako dowód iż kłamię że podawałem ci linka do angielskiej wikipedii? |
Masz kłopoty z Interpretacją najprostszych zdań?
Cytuję fragment postu wyżej:
| rafal3006 napisał: |
Zauważ Irbisolu, że definicja warunku wystarczającego => zapisana na wstępie podaje algorytm dowodu prawdziwości warunku wystarczającego => w zbiorach!
Na 100% nie ma tego algorytmu w gównie cytowanym w polskiej Wikipedii. ani też w jakiejkolwiek innej Wikipedii: Angielskiej, Chińskiej, czy Buszmeńskiej.
|
Link podawałeś, ale w tym linku na 100% nie ma algorytmu dowodzenia warunku wystarczającego => w zbiorach jak to ma miejsce w poniższej definicji warunku wystarczającego.
Kłamałeś w temacie jakoby gdziekolwiek w Wikipedii (Polskiej, Angielskiej etc) był algorytm dowodzenia warunku wystarczającego => w zbiorach, jak niżej.
2.
Definicja warunku wystarczającego => w zbiorach:
Jeśli p to q
p=>q =1
Zajście p jest (=1) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => jest (=1) spełniona wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Inaczej:
p=>q =0
Zajście p nie jest (=0) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => nie jest (=0) spełniona wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Ostatnio zmieniony przez rafal3006 dnia Wto 2:59, 22 Mar 2022, w całości zmieniany 2 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Wto 2:39, 22 Mar 2022 Temat postu: Wysłany: Wto 2:39, 22 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652401
Kto zgadnie jaka będzie odpowiedź Irbisola na niniejszy post?
Ja obstawiam taką odpowiedź:
Nie zamówionego gówna nie czytam - zapisz co chcesz powiedzieć w jednym zdaniu.
| Irbisol napisał: |
| rafal3006 napisał: | | Link podawałeś, ale w tym linku na 100% nie ma algorytmu dowodzenia warunku wystarczającego => w zbiorach jak to ma miejsce w poniższej definicji warunku wystarczającego. |
I co z tego? KRZ przyznaje, że inkluzja zbioru to warunek wystarczający. Niezależnie od tego, czy tego dowodzi, czy nie. |
[link widoczny dla zalogowanych]
| Wikpedia napisał: |
Warunek wystarczający
Warunek wystarczający (inaczej warunek dostateczny) – każdy warunek, z którego dany fakt wynika. Jeżeli warunek wystarczający zachodzi (wystarczy, by zachodził), wówczas zachodzi dany fakt.
Na przykład, jeżeli liczba jest podzielna przez 10, to jest podzielna przez 5. Fakt podzielności przez 10 jest warunkiem wystarczającym dla podzielności przez 5, natomiast fakt podzielności przez 5 jest warunkiem koniecznym dla podzielności przez 10.
Warunek wystarczający nie musi być warunkiem koniecznym — liczba nie musi wcale być podzielna przez 10, by była podzielna przez 5. |
Weźmy to wytłuszczone zdanie z Wikipedii.
Zadanka z logiki matematycznej w I klasie LO w 100-milowym lesie.
Zadanie 1.
A1.
Jeśli liczba jest podzielna przez 10 to jest podzielna przez 5
Polecenie:
Udowodnij, czy w zdaniu A1 warunek wystarczający jest spełniony/niespełniony
Zadanie 2.
B1.
Jeśli liczba jest podzielna przez 5 to jest podzielna przez 10
Polecenie:
Udowodnij, czy w zdaniu B1 warunek wystarczający jest spełniony/niespełniony
Poproszę o twoje rozwiązanie zadań 1 i 2.
Na gruncie KRZ nigdy tych zadań nie rozwiążesz.
Mam nadzieję, że wiesz co to znaczy "udowodnij".
Sam widzisz, że KRZ leży i kwiczy na najprostszych zadankach matematycznych.
cnd
P.S.
Jak to jest w KRZ?
Podpowiedź dla Irbisola.
[link widoczny dla zalogowanych]
| medianauka napisał: |
Warunek konieczny i wystarczający
Jeżeli ze zdania p wynika zdanie q, to zdanie p jest warunkiem wystarczającym (dostatecznym) dla zdania q, a zdanie q jest warunkiem koniecznym dla zdania q.
Przykład
Niech p oznacza zdanie: liczba N jest podzielna przez 10.
Niech q oznacza zdanie: liczba N jest podzielna przez 5.
Zdanie p jest warunkiem wystarczającym dla q (podzielność liczby przez 10 jest warunkiem wystarczającym podzielności liczby przez 5).
Zdanie q jest warunkiem koniecznym dla p (podzielność liczby przez 5 jest warunkiem koniecznym podzielności przez 10).
Ciekawe jest to, że zdanie q (podzielność przez 5) nie jest warunkiem wystarczającym dla p (podzielności przez 10) (na przykład dla N=15.), a także p nie jest warunkiem koniecznym dla q (na przykład liczba 5 jest podzielna przez 5, ale nie dzieli się przez 10)
Teoria:
Jeżeli warunek konieczny jest jednocześnie warunkiem wystarczającym, to mówimy wówczas, że jest to warunek konieczny i wystarczający.
Jeżeli rozbudujemy nieco powyższy przykład w taki sposób, że zdanie q będzie zdefiniowane jako: liczba N jest parzysta i podzielna przez 5, to otrzymamy przykład warunku koniecznego i wystarczającego, a mianowicie: podzielność liczby parzystej N przez 5 jest warunkiem koniecznym i wystarczającym dla podzielności liczby przez 10. |
Podsumowując:
KRZ nie ma najmniejszego pojęcia jak UDOWODNIĆ czy zdanie warunkowe "Jeśli p to q" spełnia, bądź nie spełnia definicję warunku wystarczającego =>.
Kluczowe pytanie od Irbisola:
Czy widzisz fundamentalną różnicę między definicją warunku wystarczającego rodem z KRZ (patrz cytat wyżej) a definicją warunku wystarczającego => rodem z algebry Kubusia jak niżej.
http://www.sfinia.fora.pl/forum-kubusia,12/algebra-kubusia-matematyka-jezyka-potocznego-w-trakcie,20453.html#649275
| Algebra Kubusia napisał: |
Wstęp:
1.
Definicja podzbioru =>:
Zbiór p jest podzbiorem => zbioru q wtedy i tylko wtedy gdy wszystkie elementy zbioru p należą do zbioru q
p=>q =1 - wtedy i tylko wtedy gdy relacja podzbioru => jest (=1) spełniona
Inaczej:
p=>q =0 - wtedy i tylko wtedy gdy relacja podzbioru => nie jest (=0) spełniona
Finał:
2.
Definicja warunku wystarczającego => w zbiorach:
Jeśli p to q
p=>q =1
Zajście p jest (=1) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => jest (=1) spełniona wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Inaczej:
p=>q =0
Zajście p nie jest (=0) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => nie jest (=0) spełniona wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q |
Uwaga:
Także banalna definicja podzbioru w KRZ jest totalnie spieprzona w sposób identyczny jak definicja warunku wystarczającego.
Dowód:
W KRZ definicją podzbioru p=>q nie jest relacja podzbioru => (jak w AK - patrz cytat wyżej), a goły zbiór p
Ostatnio zmieniony przez rafal3006 dnia Wto 9:33, 22 Mar 2022, w całości zmieniany 6 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Wto 17:55, 22 Mar 2022 Temat postu: Wysłany: Wto 17:55, 22 Mar 2022 Temat postu: |
|
|
Odpowiedź Irbisola na powyższy post z moim komentarzem:
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652417
Kto zgadnie jaka będzie odpowiedź Irbisola na niniejszy post?
Ja obstawiam taką odpowiedź:
Nie podam linku, sam sobie poszukaj w tonach gówna które zapisałeś.
| Irbisol napisał: | | rafal3006 napisał: | Poproszę o twoje rozwiązanie zadań 1 i 2.
Na gruncie KRZ nigdy tych zadań nie rozwiążesz. |
Pewnie nie i nie mam zamiaru.
Pisałeś, że KRZ nie wie, że inkluzje zbioru to warunek wystarczający - dostałeś link udowadniający, że wie.
Masz coś na ten temat do napisania, czy będziesz wiecznie spierdalał w inne pytania? |
Czy możesz podać ten link ponownie?
Chcę sprawdzić czy mówisz prawdę.
... a jednak podał, dziękuję:
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652429
| Irbisol napisał: | | http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141 |
Ostatnio zmieniony przez rafal3006 dnia Wto 17:57, 22 Mar 2022, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Wto 17:58, 22 Mar 2022 Temat postu: Wysłany: Wto 17:58, 22 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652473
Czy Irbisol zgodzi się podjąć rzeczową dyskusję na temat logiki matematycznej?
Moja odpowiedź:
Irbisol nigdy nie zgodzi się spojrzeć na logikę matematyczną z innego poziomu, niż z poziomu potwornie śmierdzącego gówna, zwanego Klasycznym Rachunkiem Zdań
Dowód tego faktu będzie w serii kolejnych postów.
Post Nr.1
Tu jest forum polskie, zatem nie mam zamiaru dyskutować o logice matematycznej w języku angielskim, dlatego przetłumaczyłem istotę cytatu na język polski.
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
Moje pytanie wstępne jest takie:
Czy wiesz dlaczego znalazłeś ten cytat w jednym jedynym, możliwym miejscu, w angielskiej Wikipedii, gdzie pisać mogą matematyczne jełopy?
Moja podpowiedź:
Nie najdziesz tego cytatu na żadnej stronie internetowej jakiegokolwiek szanującego się Uniwersytetu, wszystko jedno w jakim kraju, od USA po krainę Buszmenów.
Teraz proszę o twoją odpowiedź.
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Wto 22:31, 22 Mar 2022 Temat postu: Wysłany: Wto 22:31, 22 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652525
Czy ktoś ma nadzieję, iż Irbisol powie chcę?
Post Nr.3
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
| Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | Pytałeś o wikipedię i dostałeś odpowiedź. |
Ten cytat w angielskiej Wikipedii to cytat matematycznego tumana, czy chcesz bym ci to wytłumaczył na poziomie ucznia I klasy LO? |
Nie - nie chcę żebyś mi tłumaczył. Chcę, żebyś mi wskazał, które jego zdanie jest fałszywe. A tak się składa, że napisał dokładnie to, czego chciałeś.
BTW. Nadal się nie odniosłeś do faktu, że chciałeś cytat z wikipedii wiążący warunek wystarczający ze zbiorami i taki cytat dostałeś. |
Wszystkie zdania są prawdziwe, ale sens całości to głupota, napisana przez matematycznego tumana, totalnie nierozumiejącego logiki matematycznej, którego jedynym celem jest zrobienie wody w mózgach uczniów I klasy LO.
Ten diagram w zbiorach nie pasuje do żadnego z czterech możliwych spójników obsługiwanych zdaniami warunkowymi "Jeśli p to q"
p<=>q - równoważność, diagram tłuka jest fałszem
p|=>q - implikacja prosta, diagram tłuka jest fałszem
p|~>q - implikacja odwrotna, diagram tłuka jest fałszem
p|~~>q - chaos, diagram tłuka jest fałszem
Podsumowując:
Diagram tłuka jest totalnie fałszywy!
Powtórzę:
Czy chcesz, bym ci wytłumaczył na poziomie ucznia I klasy LO, iż fragment angielskiej Wikipedii to dzieło matematycznego tumana z zerowym pojęciem o logice matematycznej?
Ostatnio zmieniony przez rafal3006 dnia Śro 12:53, 23 Mar 2022, w całości zmieniany 2 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Śro 15:15, 23 Mar 2022 Temat postu: Wysłany: Śro 15:15, 23 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652561
Malunek tumana z Wikipedii to potwornie śmierdzące gówno mające zero wspólnego z logiką matematyczną.
| Irbisol napisał: | Może po prostu zaprezentuj swoją wersję.
O objętości takiej, jak to zrobił ów "tłuk" lub nieznacznie większej. |
Irbisolu,
Logika matematyczna nie polega na określaniu prawdziwości/fałszywości dowolnych zdań, ale na szukaniu matematycznych związków między tymi zdaniami.
Innymi słowy, pojedyncze zdania mogą być prawdziwe, ale całość może być gównem, jak u tego tłuka z Wikipedii.
Jedyne co mogę dla ciebie zrobić, by napisać jak najkrócej, to posłużyć się definicjami znaczków <=>, |=>, |~> i p|~~>q w zbiorach.
Po kompletna teorię odsyłam oczywiście do algebry Kubusia.
http://www.sfinia.fora.pl/forum-kubusia,12/algebra-kubusia-matematyka-jezyka-potocznego-w-trakcie,20453.html#636007
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
Dowód iż opis tłuka powyższego malunku ma zero wspólnego z logika matematyczną:
1.
Definicja równoważności p<=>q w zbiorach:
Równoważność w zbiorach to dwa i tylko dwa zbiory niepuste i rozłączne uzupełniające się do dziedziny
Definicja ogólna równoważności p<=>q w zbiorach:
A1: p=>q=1 - zbiór p jest (=1) podzbiorem => zbioru q
B1: p~>q=1 - zbiór p jest (=1) nadzbiorem ~> zbioru q
Stąd:
p<=>q = (A1: p=>q)*(B1: p~>q)
Czytamy:
Definicja równoważności p<=>q jest spełniona wtedy i tylko wtedy gdy zbiór p jest nadzbiorem ~> (B1) zbioru q i jednocześnie zbiór p jest podzbiorem => (A1) zbioru q
W algebrze Kubusia w zbiorach zachodzi tożsamość pojęć:
Warunek wystarczający A1: p=>q = relacja podzbioru A1: p=>q = twierdzenie proste p=>q=~p+q
##
Warunek konieczny B1: p~>q = relacja nadzbioru B1: p~>q = twierdzenie odwrotne B3: q=>p=~q+p
bo prawo Tygryska:
B1: p~>q = B3: q=>p = p+~q
Gdzie:
## - różne na mocy definicji
p i q musi być wszędzie tymi samymi p i q, inaczej błąd podstawienia
Stąd mamy tożsamą definicje równoważności p<=>q:
A1: p=>q=1 - zajście p jest (=1) wystarczające => dla zajścia q
B1: p~>q=1 - zajście p jest (=1) konieczne ~> dla zajścia q
Stąd:
p<=>q = (A1: p=>q)*(B1: p~>q)
Czytamy:
Definicja równoważności p<=>q jest spełniona wtedy i tylko wtedy gdy zajście p jest konieczne (B1) i wystarczające => (A1) dla zajścia q
To jest podstawowa definicja równoważności doskonale znana wszystkim ludziom (w tym matematykom).
Dowód:
Klikamy na googlach:
„konieczne i wystarczające”
Wyników: 8 140
„Potrzeba i wystarcza”
Wyników: 49 000
Przykład:
Dowolny człowiek jest mężczyzną (M) wtedy i tylko wtedy gdy nie jest kobietą (~K)
C=M+K - dziedzina C (człowiek) to suma logiczna zbiorów M+K, zbiorów uzupełniających się do dziedziny C
Mamy tu następującą równoważność:
M<=>~K = (A1: M=>~K)*(B1: M~>~K)
Czytamy:
Równoważność M<=>~K jest spełniona (=1) wtedy i tylko wtedy gdy bycie mężczyzną jest warunkiem koniecznym ~> (B1) i wystarczającym => (A1), aby nie być kobietą (~K)
Podstawmy dla powyższego gówno-malunku:
M (mężczyzna) = zbiór A
K (kobieta) = zbiór B
Po takim podstawieniu rysunek tumana z Wikipedii stwierdza, iż zbiór mężczyzn (M) ma co najmniej jeden element wspólny ze zbiorem kobiet (K), czyli w naszym świecie rzeczywistym istnieje „mężczyzno-kobieta”
Wniosek:
Malunek tumana w angielskiej Wikipedii ma zero wspólnego z definicją równoważności w zbiorach
W identyczny sposób rysunek tumana z Wikipedii jest sprzeczny z pozostałymi możliwymi spójnikami opisującymi zdania warunkowe „Jeśli p to q”
2.
Implikacja prosta p|=>q w zbiorach:
Zbiór p jest podzbiorem => zbioru q i nie jest tożsamy ze zbiorem q
Dziedzina musi być szersza od sumy logicznej zbiorów p+q
W malunku tumana z Wikipedii musimy tu podstawić
p=A*B
q=A
oraz wymazać gumką niebieską część zbioru B
Wniosek:
Malunek tumana w angielskiej Wikipedii ma zero wspólnego z definicją implikacji prostej p|=>q w zbiorach
3.
Implikacja odwrotna p|~>q w zbiorach:
Zbiór p jest nadzbiorem ~> zbioru q i nie jest tożsamy ze zbiorem q
Dziedzina musi być szersza od sumy logicznej zbiorów p+q
W malunku tumana z Wikipedii musimy u podstawić:
p=A
q=A*B
oraz wymazać gumką niebieską część zbioru B
Wniosek:
Malunek tumana w angielskiej Wikipedii ma zero wspólnego z definicją implikacji odwrotnej p|~>q w zbiorach
3.
Chaos p|~~>q w zbiorach:
Zbiór p ma część wspólną ze zbiorem q i żaden z nich nie jest podzbiorem => drugiego
W tym przypadku dziedzina to cztery zbiory niepuste i rozłączne uzupełniające się do dziedziny D
D= A: p*q + B: p*~q + C:~p*q + D: ~p*~q
Podstawmy:
p=A
q=B
W tym przypadku zbiory A,B,C pasują do malunku tumana z Wikipedii, ale nie ma na nim zbioru niepustego D!
D=~(A+B) = ~A*~B
Wniosek:
Malunek tumana w angielskiej Wikipedii ma zero wspólnego z definicją chaosu p|~~>q w zbiorach
Podsumowując:
Malunek tumana z Wikipedii to potwornie śmierdzące gówno mające zero wspólnego z logiką matematyczną obowiązującą w naszym Wszechświecie
cnd
Ostatnio zmieniony przez rafal3006 dnia Śro 15:38, 23 Mar 2022, w całości zmieniany 2 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Śro 17:57, 23 Mar 2022 Temat postu: Wysłany: Śro 17:57, 23 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652587
Najpopularniejszy rysunek logiki matematycznej w ziemskich podręcznikach matematyki jest rysunkiem tłuka
Podsumowując:
Najpopularniejszy rysunek logiki matematycznej w ziemskich podręcznikach matematyki (jak niżej) jest rysunkiem tłuka (jest gównem) bo nie przedstawia poprawnie w zbiorach żadnego z operatorów logicznych, nawet OR(|+) i AND(|*)
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
| Irbisol napisał: | "Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne"
- to ma być potworne gówno? |
Czytaj ze zrozumieniem:
To zdanie jest prawdziwe ale cały rysunek tłuka jest gównem, bo nie opisuje poprawnie żadnego operatora logicznego w zbiorach.
To jest gówno rysunek nawet w stosunku do operatora OR(|+) i AND(|*) bo brakuje na min zbioru niepustego ~(A+B)
~(A+B)=~A*~B
Co więcej:
Wszelkie rysunki tego typu, a jest ich w ziemskiej logice zatrzęsienie, z punktu widzenia operatorów logicznych są gównem.
Dowód:
Brak zbioru/zdarzenia niepustego ~A*~B widzi każdy 5-cio latek, tylko ziemscy matematycy nie mają pojęcia że on musi być na powyższym malunku by poprawnie opisać operator OR(|+).
Definicja operatora OR(|+):
Operator OR(|+) to układ równań logicznych 1 i 2 dający odpowiedź na pytanie o Y i ~Y:
1.
Y=p+q
... a kiedy zajdzie ~Y?
Negujemy 1 dwustronnie:
~Y=~(p+q)=~p*~q
stąd mamy:
2.
~Y=~p*~q
Przykład z przedszkola.
Pani w przedszkolu:
1.
Jutro pójdziemy do kina (K) lub do teatru (T)
Y = K+T
Czytamy:
Pani dotrzyma słowa (Y) wtedy i tylko wtedy gdy juto pójdziemy do kina (K) lub do teatru (T)
... a kiedy pani nie dotrzyma słowa (~Y)?
Negujemy 1 stronami:
2.
~Y=~K*~T
Czytamy:
Pani nie dotrzyma słowa (~Y) wtedy i tylko wtedy gdy jutro nie pójdziemy do kina (~K) i nie pójdziemy do teatru (~T)
Jak widzimy, możliwe jest jednoczesne zajście zdarzeń:
Jutro nie pójdziemy do kina (~K) i nie pójdziemy do teatru (~T)
bo chwilą czasową jest tu cały jutrzejszy dzień
... a na rysunku tłuka z Wikipedii nie ma zdarzenia możliwego ~K*~T - dlatego to rysunek tłuka.
cnd
Podsumowując:
Najpopularniejszy rysunek logiki matematycznej w ziemskich podręcznikach matematyki jest rysunkiem tłuka (jest gównem) bo nie przedstawia poprawnie w zbiorach żadnego z operatorów logicznych, nawet OR(|+) i AND(|*)
Ostatnio zmieniony przez rafal3006 dnia Śro 18:28, 23 Mar 2022, w całości zmieniany 2 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Śro 18:48, 23 Mar 2022 Temat postu: Wysłany: Śro 18:48, 23 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652609
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
| Irbisol napisał: | | Ale ty mi nie pisz, czego tu brakuje. Napisz, co jest błędne. |
Z punktu widzenia opisu operatorów logicznych w zbiorach/zdarzeniach zachodzi tożsamość:
brakuje = błędne
Innymi słowy:
Na wszelkich malunkach w zbiorach/zdarzeniach opisujących operatory logiczne muszą być naniesione wszelkie cechy charakterystyczne dla danego operatora, inaczej malunek jest błędny.
W dwóch ostatnich postach udowodniłem, że najsłynniejszy malunek logiki matematycznej (patrz rysunek wyżej) jest z punktu odniesienia opisu operatorów logicznych totalnie błędny, bo nie opisuje poprawnie ani jednego operatora logicznego.
Przykład:
Człowiek ma serce i osioł ma serce.
Czy możesz na polecenie pani przedszkolanki "Narysuj człowieka" narysować osła?
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Śro 21:27, 23 Mar 2022 Temat postu: Wysłany: Śro 21:27, 23 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652641
| Irbisol napisał: | Czyli błędu nie znalazłeś.
cnd |
W obszarze operatorów logicznych których rzeczony malunek ma dotyczyć znalazłem sześć fundamentalnych błędów.
Dowód w niniejszym poście.
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652561
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652587
W powyższych linkach udowodniłem iż najsłynniejszy malunek logiki matematycznej (jak niżej) jest z punktu widzenia operatorów logicznych totalnie błędny, bo nie opisuje poprawnie żadnego z sześciu operatorów logicznych.
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
W dalszym opisie podstawiam:
A=p
B=q
by być w powszechnie przyjętym standardzie logiki matematycznej.
I.
OR(|+):
1.
Y=p+q
2.
~Y=~p*~q
Nie ma członu ~p*~q na powyższym malunku, dlatego jest on matematycznie błędny
cnd
II
AND(|*):
1.
Y=p*q
2.
~Y=~(p*q)=~p+~q
Definicja spójnika „lub”(+) w zbiorach/zdarzeniach rozłącznych:
p+q = p*q+p*~q + ~p*q
stąd mamy:
~Y=~p+~q = ~p*~q + ~p*q + p*q
Nie ma członu ~p*~q na powyższym malunku, dlatego jest on matematycznie błędny
cnd
III.
Równoważność p<=>q:
A1: p=>q=1 - zbiór p jest (=1) podzbiorem => zbioru q
B1: p~>q=1 - zbiór p jest (=1) nadzbiorem ~> zbioru q
p<=>q = (A1: p=>q)*(B1: p~>q)=1*1=1
Definicja tożsamości zbiorów p=q:
Zbiór p jest tożsamy ze zbiorem q (p=q) wtedy i tylko wtedy gdy jest jednocześnie podzbiorem => q (A1) i nadzbiorem ~>q (B1)
p=q <=> (A1: p=>q)*(B1: p~>q)=1*1=1
Na powyższym malunku nie zachodzi tożsamość zbiorów p=q wymuszająca tożsamość zbiorów ~p=~q
Wniosek:
Powyższy malunek jest błędny dla równoważności p<=>q
cnd
IV.
Implikacja prosta p|=>q:
A1: p=>q=1 - zbiór p jest (=1) podzbiorem => zbioru q
B1: p~>q=0 - zbiór p nie jest (=0) nadzbiorem ~> zbioru q
p|=>q = (A1: p=>q)*~(B1: p~>q)=1*~(0)=1*1=1
Wniosek:
Zbiór p jest podzbiorem => zbioru q i nie jest tożsamy ze zbiorem q
Dziedzina musi być szersza od sumy logicznej zbiorów p+q
Nie ma tego na powyższym malunku, zatem jest on błędny dla p|=>q
cnd
V.
Implikacja odwrotna p|~>q:
A1: p=>q=0 - zbiór p nie jest (=0) podzbiorem => zbioru q
B1: p~>q=1 - zbiór p jest (=1) nadzbiorem ~> zbioru q
p|~>q = ~(A1: p=>q)*(B1: p~>q)=~(0)*1=1*1=1
Wniosek:
Zbiór p jest nadzbiorem ~> zbioru q i nie jest tożsamy ze zbiorem q
Dziedzina musi być szersza od sumy logicznej zbiorów p+q
Nie ma tego na powyższym malunku, zatem jest on błędny dla p|~>q
cnd
VI
Chaos p|~~>q:
A1: p=>q=0 - zbiór p nie jest (=0) podzbiorem => zbioru q
B1: p~>q=0 - zbiór p nie jest (=0) nadzbiorem ~> zbioru q
p|~~>q = ~(A1: p=>q)*~(B1: p~>q)=~(0)*~(0)=1*1=1
Wniosek:
Zbiory p i q mają element wspólny i żaden z niech nie zawiera się w drugim
Tą definicję malunek prawie spełnia bo brakuje tylko zbioru niepustego ~p*~q
Prawie, robi fundamentalną różnicę
Wniosek:
Malunek błędnie opisuje chaos p|~~>q
cnd
Ostatnio zmieniony przez rafal3006 dnia Śro 21:36, 23 Mar 2022, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Czw 15:55, 24 Mar 2022 Temat postu: Wysłany: Czw 15:55, 24 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652715
Jedyny, poprawny diagram operatora OR(|+)=(Y|=p+q) w zdarzeniach/zbiorach!
Operator OR(|+) = Y|=p+q
Operator OR(|+) to nie jest goły spójnik "lub"(+) Y=p+q
| Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | rafal3006 napisał: | | W powyższych linkach udowodniłem iż najsłynniejszy malunek logiki matematycznej (jak niżej) jest z punktu widzenia operatorów logicznych totalnie błędny, bo nie opisuje poprawnie żadnego z sześciu operatorów logicznych. |
Czyli opisuje je błędnie? |
Tak, opisuje je błędnie. |
W jaki zatem sposób opisuje operator OR? |
Zacznijmy od tego że żaden ziemianin nie zna poprawnej definicji operatora OR(|+)
Cytuję fragment AK mówiący o poprawnej definicji operatora OR(|+) oraz przedstawiający poprawny diagram operatora OR(|+) w zdarzeniach/zbiorach.
Czy możesz napisać co ci się nie podoba, co kwestionujesz?
Jeśli znajdziesz błąd czysto matematyczny to oczywiście kasuję calusieńką AK!
http://www.sfinia.fora.pl/forum-kubusia,12/algebra-kubusia-matematyka-jezyka-potocznego-w-trakcie,20453.html#641805
4.1 Operator A1: Y|=p+q wyrażony spójnikami „i”(*) i „lub”(+)
Częstotliwość użycia w języku potocznym: bardzo duża
Definicja matematyczna operatora A1: Y|=p+q w spójnikach „i”(*) i „lub”(+):
Definicja matematyczna operatora A1: Y|=p+q wyrażonego spójnikami „i”(*) i „lub”(+) jest spełniona wtedy i tylko wtedy gdy wszystkie możliwe człony funkcji logicznej Y i ~Y przyjmują wartość logiczną 1.
Definicja fizyczna operatora Y|=p+q w spójnikach „i”(*) i „lub”(+):
Definicja fizyczna operatora Y|=p+q wyrażonego spójnikami „i”(*) i „lub”(+) jest spełniona wtedy i tylko wtedy gdy iloczyny logiczne zdarzeń/zbiorów p i q przez wszystkie możliwe przeczenia p i q będą zdarzeniami możliwymi ~~> lub zbiorami niepustymi ~~>.
Innymi słowy:
Definicja fizyczna operatora Y|=p+q wyrażonego spójnikami „i”(*) i „lub”(+) jest spełniona wtedy i tylko wtedy gdy na mocy teorii zbiorów/zdarzeń nie da się zredukować ani funkcji logicznej Y ani też funkcji logicznej ~Y
Definicja matematyczna operatora Y|=p+q to układ równań logicznych Y i ~Y:
1.
Y=p+q
co w logice jedynek oznacza:
Y=1 <=> p=1 lub q=1
.. a kiedy zajdzie ~Y?
Negujemy równanie 1 stronami:
2.
~Y=~p*~q
co w logice jedynek oznacza:
~Y=1 <=> ~p=1 i ~q=1
Definicja spójnika „lub”(+) w zdarzeniach/zbiorach rozłącznych:
p+q = p*q + p*~q + ~p*q
Stąd mamy tożsamą funkcję logiczną Y w logice dodatniej (bo Y):
1’
Y = A: p*q+ B: p*~q + C: ~p*q
Dowód:
Minimalizujemy funkcję 1’:
Y = p*q + p*~q + ~p*q
Y = p*(q+~q)+~p*q
Y = p+(~p*q)
Przejście do logiki ujemnej (bo ~Y) poprzez negację zmiennych i wymianę spójników:
~Y = ~p*(p+~q)
~Y = ~p*p+~p*~q
~Y=~p*~q
Powrót do logiki dodatniej (bo Y) poprzez negację zmiennych i wymianę spójników:
Y = p+q
cnd
Stąd mamy:
1: Y=p+q [=] 1’: Y = A: p*q+ B: p*~q + C: ~p*q
Diagram w zdarzeniach opisujący ten przypadek jest następujący:
| Kod: |
D1
Definicja operatora A1: Y|=p+q w zdarzeniach
--------------------------------------------------------------------------
| D=p*q+p*~q+~p*q+~p*~q=1 - dziedzina, suma logiczna zdarzeń rozłącznych |
--------------------------------------------------------------------------
| p |
------------------------------------------------------
| q |
--------------------------------------------------------------------------
| B: Yb=p*~q | A: Ya=p*q | C: Yc=~p*q | D:~Yd=~p*~q |
--------------------------------------------------------------------------
|
Zdarzenia ABCD to zdarzenia niepuste i rozłączne uzupełniające się wzajemnie do dziedziny D
Dowód wzajemnej rozłączności zdarzeń ABCD:
A: p*q
B: p*~q
C: ~p*q
D: ~p*~q
Mnożymy logicznie każde zdarzenie z każdym:
A*B=(p*q)*(p*~q)=[] =0 - bo q*~q=0
A*C=(p*q)*(~p*q)=[] =0 - bo p*~p=0
A*D=(p*q)*(~p*~q)=[]=0 - bo p*~p=0
B*C=(p*~q)*(~p*q)=[]=0 - bo p*~p=0
B*D=(p*~q)*(~p*~q)=[]=0 - bo p*~p=0
C*D=(~p*q)*(~p*~q)=[]=0 - bo q*~q=[]=0
cnd
Dowód iż zdarzenia ABCD uzupełniają się wzajemnie do dziedziny D:
D = A: p*q + B: p*~q + C: ~p*q + D: ~p*~q
D=p*q + p*~q + ~p*q + ~p*~q
D=p*(q+~q) + ~p*(q+~q)
D=p+~p =1
cnd
Przykład:
Dowolną funkcję logiczną Y mamy prawo tylko i wyłącznie dwustronnie zanegować:
1.
Y = p+q
co w logice jedynek oznacza:
Y=1 <=> p=1 lub q=1
bo w równaniach alternatywno-koniunkcyjnych jedynki są domyślne.
Matematyczna definicja spójnika „lub”(+) w zdarzeniach/zbiorach rozłącznych odczytana z diagramu D1 to:
Y=Ya+Yb+Yc
Po rozwinięciu mamy:
Y = p+q = A: p*q + B: p*~q + C:~p*q
Czyli:
1’
Y = A: p*q + B: p*~q + C:~p*q
co w logice jedynek oznacza:
Y=1 <=> A: p=1 i q=1 lub B: p=1 i ~q=1 lub C: ~p=1 i q=1
#
2.
… a kiedy zajdzie ~Y?
Negujemy dwustronnie równanie 1:
~Y = ~(p+q) = ~p*~q - na mocy prawa De Morgana.
co w logice jedynek oznacza:
~Y=1 <=> ~p=1 i ~q=1
bo w równaniach alternatywno-koniunkcyjnych jedynki są domyślne.
Gdzie:
# - różne w znaczeniu iż dowolna strona znaczka # jest negacją drugiej strony
W definicji fizycznej operatora Y|=p+q wyrażonego spójnikami „i”(*) i „lub”(+) chodzi o to by na mocy teorii zdarzeń/zbiorów nie dało się wyrugować dowolnego z członów ABC powyższej definicji
Przykładowo dla:
A: p*q=[]=0 - gdy zdarzenia/zbiory p i q są rozłączne
mamy:
Y = p+q = A: p*q + B: p*~q + C: ~p*q ## B: p*~q + C: ~p*q = p$q
Gdzie:
## - różne na mocy definicji ##
$ - spójnik „albo”($) z języka potocznego człowieka
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Czw 17:02, 24 Mar 2022 Temat postu: Wysłany: Czw 17:02, 24 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1575.html#652727
Czy Irbisol jest w stanie przeczytać ze zrozumieniem tekst na poziomie 5-cio letniego dziecka?
Doskonale wyjaśniający definicję operatora „lub”(|+)=(Y|=p+q).
Moja odpowiedź:
Irbisol nigdy nie przeczyta ze zrozumieniem niniejszego postu na poziomie 5-cio letniego dziecka.
Dlaczego?
Bo jest matematycznie bajecznie prosty, perfekcyjny i nie do obalenia.
Irbisol czyta tylko te posty do których może się przyczepić, innych z definicji nie czyta.
| Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | rafal3006 napisał: | | W powyższych linkach udowodniłem iż najsłynniejszy malunek logiki matematycznej (jak niżej) jest z punktu widzenia operatorów logicznych totalnie błędny, bo nie opisuje poprawnie żadnego z sześciu operatorów logicznych. |
Czyli opisuje je błędnie? |
Tak, opisuje je błędnie. |
W jaki zatem sposób opisuje operator OR? |
Zacznijmy od tego że żaden ziemianin nie zna poprawnej definicji operatora OR(|+) |
Zacznijmy od tego, żebyś odpowiedział na pytanie. |
Na to wytłuszczone pytanie konieczną teorię wyłożyłem w moim poście wyżej, nie da się na twoje wytłuszczone pytanie odpowiedzieć jednym zdaniem, jakbyś tego oczekiwał.
Zacznijmy od tego byś zrozumiał teorię operatora OR(|+)=(Y|=p+q) na przykładzie z przedszkola, wyłożoną w niniejszym poście.
Czy przeczytasz?
…
Fragment AK:
http://www.sfinia.fora.pl/forum-kubusia,12/algebra-kubusia-matematyka-jezyka-potocznego-w-trakcie,20453.html#641805
4.1.1 Przykład operatora Y|=K+T w zdarzeniach
Częstotliwość użycia w języku potocznym: bardzo duża
Rozważmy zdanie na poziomie 5-cio letniego dziecka.
Pani przedszkolanka:
1.
ABC:
Jutro pójdziemy do kina lub do teatru
Y=K+T
co w logice jedynek oznacza:
Y=1 <=> K=1 lub T=1
Czytamy:
Pani dotrzyma słowa (Y=1) wtedy i tylko wtedy gdy jutro pójdziemy do kina (K=1) lub do teatru (T=1)
Y=K+T
co w logice jedynek oznacza:
Y=1 <=> K=1 lub T=1
Matematycznie oznacza to że jutro pójdziemy w dowolne miejsce i już pani dotrzyma słowa, czyli:
ABC:
Y=A: K*T + B: K*~T + C:~K*T
co w logice jedynek oznacza:
Y=1 <=> A: K=1 i T=1 lub B: K=1 i ~T=1 lub C: ~K=1 i T=1
Czytamy:
Pani dotrzyma słowa (Y=1) wtedy i tylko wtedy gdy:
A: Ya=K*T=1*1 =1 - jutro pójdziemy do kina (K=1) i do teatru (T=1)
LUB
B: Yb=K*~T=1*1 =1 - jutro pójdziemy do kina (K=1) i nie pójdziemy do teatru (~T=1)
LUB
C: Yc=~K*T=1*1 =1 - jutro nie pójdziemy do kina (~K=1) i pójdziemy do teatru (T=1)
Matematycznie zachodzi tożsamość funkcji logicznych:
Y = Ya+Yb+Yc
Gdzie:
Ya, Yb, Yc - funkcje cząstkowe wchodzące w skład funkcji Y
Przejdźmy na zapisy formalne podstawiając:
K=p
T=q
Dowód iż tak jest w istocie w zapisach formalnych.
stąd:
Y = Ya+Yb+Yc = A: p*q + B: p*~q + C: ~p*q
minimalizujemy funkcję logiczną Y:
Y = p*q + p*~q + ~p*q
Y = p*(q+~q) + ~p*q
Y = p+(~p*q)
Przejście do logiki ujemnej (bo ~Y) poprzez negację zmiennych i wymianę spójników:
~Y = ~p*(p+~q)
~Y = ~p*p + ~p+~q
~Y = ~p*~q
Powrót do logiki dodatniej poprzez negację zmiennych i wymianę spójników:
Y = p+q
co w logice jedynek oznacza:
Y=1 <=> p=1 lub q=1
cnd
Matematycznie zachodzi:
Y=Y
stąd mamy definicję spójnika „lub”(+) w zdarzeniach rozłącznych ABC którą warto zapamiętać
Definicja spójnika “lub”(+) w zdarzeniach rozłącznych:
p+q = p*q + p*~q +~p*q
… a kiedy pani skłamie (~Y=1)?
2.
Negujemy równanie 1 (ABC) dwustronnie:
D: ~Y=~K*~T
co w logice jedynek oznacza:
D: ~Y=1 <=> ~K=1 i ~T=1
Czytamy:
D.
Pani skłamie (~Y=1) wtedy i tylko wtedy gdy jutro nie pójdziemy do kina (~K=1) i nie pójdziemy do teatru (~T=1)
D: ~Y=~K*~T
co w logice jedynek oznacza:
D: ~Y=1 <=> ~K=1 i ~T=1
| Kod: |
D1
Definicja operatora A1: Y|=K+T w zdarzeniach
--------------------------------------------------------------------------
| D=K*T+K*~T+~K*T+~K*~T=1 - dziedzina, suma logiczna zdarzeń możliwych |
--------------------------------------------------------------------------
| p=[K] |
------------------------------------------------------
| q=[T] |
--------------------------------------------------------------------------
| B: Yb=p*~q= K*~T| A: Ya=p*q=K*T | C: Yc=~p*q=~K*T | D:~Yd=~p*~q=~K*~T |
--------------------------------------------------------------------------
|
Zauważmy, że wszystkie możliwe zdarzenia ABCD są rozłączne i niepuste oraz uzupełniają się wzajemnie do dziedziny.
Dziedziną dla naszego przykładu jest zbiór wszystkich możliwych zdarzań które jutro mogą wystąpić:
D = |Ya|+|Yb|+|Yc|+|Yd|
Gdzie:
|Yx| - funkcja logiczna Yx z pominięciem przeczenia (wartość bezwzględna)
Stąd mamy:
Y = A: p*q + B: p*~q + C: ~p*q + D: ~p*~q
Minimalizujemy:
Y = p*(q+~q) + ~p*(q+~q)
Y = p+~p =1
Dziedzina jest poprawna.
cnd
W dniu jutrzejszym ma szansę wystąpić wyłącznie jedno z powyższych zdarzeń.
Dla naszego przykładu w zapisach ogólnych mamy:
p=K
q=T
Innymi słowy:
A:
Ya=p~~>q=p*q=1*1=1
Ya=K~~>T=K*T =1*1=1
Możliwe ~~> jest (=1) zdarzenie: jutro pójdziemy do kina (K=1) i do teatru (T=1)
Pani dotrzyma słowa:
Ya=1
B:
Yb=p~~>~q=p*~q=1*1=1
Yb=K~~>~q=K*~T=1*1=1
Możliwe jest (=1) zdarzenie: jutro pójdziemy do kina (K=1) i nie pójdziemy do teatru (~T=1)
Pani dotrzyma słowa:
Yb=1
C:
Yc=~p~~>q=~p*q=1*1=1
Yc=~K~~>~T=~K*T =1*1=1
Możliwe jest (=1) zdarzenie: jutro nie pójdziemy do kina (~K=1) i pójdziemy do teatru (T=1)
Pani dotrzyma słowa:
Yc=1
D:
~Yd=~p~~>~q=~p*~q=1*1=1
~Yd=~K~~>~T=~K*~T =1*1=1
Pani skłamie:
~Yd=1
Czytamy:
P1: Prawdą jest (=1), że jutro pani skłamie (~Yd), jeśli nie pójdziemy do kina (~K=1) i nie pójdziemy do teatru (~T=1)
Prawo Prosiaczka:
P1: (~Yd=1) = P2: (Yd=0)
Prawą stronę czytamy:
P2: Fałszem jest (=0), jutro że pani dotrzyma słowa (Yd), jeśli nie pójdziemy do kina (~K=1) i nie pójdziemy do teatru (~T=1)
Tożsamość zdań P1=P2 jest oczywista, co jest potwierdzeniem prawa Prosiaczka.
Ostatnio zmieniony przez rafal3006 dnia Czw 19:10, 24 Mar 2022, w całości zmieniany 2 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Czw 19:08, 24 Mar 2022 Temat postu: Wysłany: Czw 19:08, 24 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#652745
Irbisol - do bólu przewidywalny, czyta tylko te odpowiedzi które są zgodne z jego „widzi mi się”
| Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | rafal3006 napisał: | | W powyższych linkach udowodniłem iż najsłynniejszy malunek logiki matematycznej (jak niżej) jest z punktu widzenia operatorów logicznych totalnie błędny, bo nie opisuje poprawnie żadnego z sześciu operatorów logicznych. |
Czyli opisuje je błędnie? |
Tak, opisuje je błędnie. |
W jaki zatem sposób opisuje operator OR? |
Zacznijmy od tego że żaden ziemianin nie zna poprawnej definicji operatora OR(|+) |
Zacznijmy od tego, żebyś odpowiedział na pytanie. |
Na to wytłuszczone pytanie konieczną teorię wyłożyłem w moim poście wyżej, nie da się na twoje wytłuszczone pytanie odpowiedzieć jednym zdaniem, jakbyś tego oczekiwał.
Zacznijmy od tego byś zrozumiał teorię operatora OR(|+)=(Y|=p+q) na przykładzie z przedszkola, wyłożoną w niniejszym poście. |
Ty w ogóle rozumiesz, o co pytam, czy już cię do cna popierdzieliło?
Pytam, jak opisuje operator OR angielska Wikipedia, do której dałem link (podobno opisuje błędnie). Twoja teoria z AK nie ma tu zastosowania. |
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
Jak wygląda definicja operatora OR(|+) i jej poprawne rozumienie wyłożyłem ci na przykładzie zrozumiałym dla 5-cio latka w moim poście wyżej.
Irbisolu, udowodnij iż opis z cytatu, zaczerpnięty z angielskiej Wikipedii ma cokolwiek wspólnego z operatorem OR(|+).
Jak to udowodnisz, to oczywistym jest, że kasuję calusieńką algebrę Kubusia - spełni się twoje odwieczne marzenie.
Ale najpierw udowodnij!
Podpowiedź:
Zacznij od poziomu 5-cio latka.
Pani w przedszkolu:
Jutro pójdziemy do kina lub do teatru
Operator OR(|+) daje nam odpowiedź na dwa pytania:
1.
Kiedy jutro pani dotrzyma słowa?
2.
Kiedy jutro pani skłamie?
Odpowiedz na powyższe pytania.
Czas START!
P.S.
Jak odpowiesz na powyższe pytania na podstawie gówno-opisu operatora OR(|+) z angielskiej Wikipedii to kasuję calusieńką algebrę Kubusia - spełni się twoje odwieczne marzenie.
Ostatnio zmieniony przez rafal3006 dnia Czw 19:24, 24 Mar 2022, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pią 11:15, 25 Mar 2022 Temat postu: Wysłany: Pią 11:15, 25 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#652785
Pytanie o rybce, odpowiedź o pipce
| Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | Pytam, jak opisuje operator OR angielska Wikipedia, do której dałem link (podobno opisuje błędnie). Twoja teoria z AK nie ma tu zastosowania. |
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
Jak wygląda definicja operatora OR(|+) i jej poprawne rozumienie wyłożyłem ci na przykładzie zrozumiałym dla 5-cio latka w moim poście wyżej.
Irbisolu, udowodnij iż opis z cytatu, zaczerpnięty z angielskiej Wikipedii ma cokolwiek wspólnego z operatorem OR(|+). |
A po co mam to udowadniać?
Ty stwierdziłeś, że ten opis ów operator opisuje i robi to błędnie. Zatem wskaż ten opis oraz konkretny błąd.
Ty postawiłeś tezę, więc to ty ją udowadniaj. |
Co do wytłuszczonego:
Nigdy nie stwierdziłem iż powyższy malunek poprawnie opisuje operator OR(|+).
Malunek z Wikipedii nie opisuje poprawnie operatora OR(|+) bo nie ma na mim zdarzenia/zbioru niepustego:
~(A+B)=~A*~B
zatem ten malunek jest czysto matematycznym fałszem w stosunku do operatora OR(|+)
Część I
Pytanie o rybkę
Pani w I klasie LO:
Jasiu, opowiedz nam o operatorze OR(|+) na podstawie zdania
ABC:
Jutro pójdziemy do kina lub do teatru
Odpowiedź Jasia o rybce:
http://www.sfinia.fora.pl/forum-kubusia,12/algebra-kubusia-matematyka-jezyka-potocznego-w-trakcie,20453.html#641805
4.1.1 Przykład operatora Y|=K+T w zdarzeniach
Częstotliwość użycia w języku potocznym: bardzo duża
Definicja operatora OR(|+) = (Y|=p+q):
Operator OR(||+) to odpowiedź na dwa pytania o Y i ~Y
1.
Y=p+q
co w logice jedynek oznacza:
Y=1 <=> p=1 lub q=1
… a kiedy zajdzie ~Y?
Negujemy równanie 1 dwustronnie:
~Y=~(p+q)=~p*~q
stąd mamy:
2.
~Y=~p*~q
co w logice jedynek oznacza:
~Y=1 <=> ~p=1 i ~q=1
Rozważmy zdanie na poziomie 5-cio letniego dziecka.
Pani przedszkolanka:
1.
ABC:
Jutro pójdziemy do kina lub do teatru
Y=K+T
co w logice jedynek oznacza:
Y=1 <=> K=1 lub T=1
Czytamy:
Pani dotrzyma słowa (Y=1) wtedy i tylko wtedy gdy jutro pójdziemy do kina (K=1) lub do teatru (T=1)
Y=K+T
co w logice jedynek oznacza:
Y=1 <=> K=1 lub T=1
… a kiedy pani skłamie (~Y=1)?
2.
Negujemy równanie 1 (ABC) dwustronnie:
D: ~Y=~K*~T
co w logice jedynek oznacza:
D: ~Y=1 <=> ~K=1 i ~T=1
Czytamy:
D.
Pani skłamie (~Y=1) wtedy i tylko wtedy gdy jutro nie pójdziemy do kina (~K=1) i nie pójdziemy do teatru (~T=1)
D: ~Y=~K*~T
co w logice jedynek oznacza:
D: ~Y=1 <=> ~K=1 i ~T=1
| Kod: |
D1
Definicja operatora A1: Y|=K+T w zdarzeniach
--------------------------------------------------------------------------
| D=K*T+K*~T+~K*T+~K*~T=1 - dziedzina, suma logiczna zdarzeń możliwych |
--------------------------------------------------------------------------
| p=[K] |
------------------------------------------------------
| q=[T] |
--------------------------------------------------------------------------
| B: Yb=p*~q= K*~T| A: Ya=p*q=K*T | C: Yc=~p*q=~K*T | D:~Yd=~p*~q=~K*~T |
--------------------------------------------------------------------------
|
Zauważmy, że wszystkie możliwe zdarzenia ABCD są rozłączne i niepuste oraz uzupełniają się wzajemnie do dziedziny.
Część II
Odpowiedź Irbisola o pipce
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Jeszcze jakieś Ameryki masz w zanadrzu? |
To samo pytanie w I klasie LO pani kieruje do Irbisola:
Irbisolu, opowiedz nam o operatorze OR(|+) na podstawie zdania
ABC:
Jutro pójdziemy do kina lub do teatru
Odpowiedź Irbisola:
Operator OR(|+) to nie jest odpowiedź na dwa pytania:
1.
Kiedy jutro pani dotrzyma słowa
2.
Kiedy jutro pani skłamie
Jak to twierdzi głupi Jas wyżej.
Irbisolowa definicja operatora OR(|+):
Operator OR(|+) mówi nam o warunkach wystarczających => i koniecznych ~> występujących w zdaniu ABC.
| Kod: |
D1
Definicja operatora A1: Y|=K+T w zdarzeniach
--------------------------------------------------------------------------
| D=K*T+K*~T+~K*T+~K*~T=1 - dziedzina, suma logiczna zdarzeń możliwych |
--------------------------------------------------------------------------
| p=[K] |
------------------------------------------------------
| q=[T] |
--------------------------------------------------------------------------
| B: Yb=p*~q= K*~T| A: Ya=p*q=K*T | C: Yc=~p*q=~K*T | D:~Yd=~p*~q=~K*~T |
--------------------------------------------------------------------------
|
Zapiszmy początkową serię zdań prawdziwych na gruncie algebry Kubusia:
1.
Pójście do kina (K) jest (=1) warunkiem koniecznym => by pójść do kina i do teatru (K*T)
K~>K*T =1
To zdanie jest prawdziwe w AK, ale ma zero wspólnego z definicją operatora OR(|+) podaną przez Jasia wyżej.
Innymi słowy: odpowiedź Irbisola jest o pipce
2.
Pójście do kina (K) nie jest (=0) warunkiem wystarczającym => aby pójść do kina i do teatru (K*T)
K=>K*T =0
bo jutro możemy nie pójść do teatru, wtedy będzie:
K*T=[]=0
stąd:
K=>[] =0
To zdanie jest fałszywe na gruncie AK, ale ma zero wspólnego z definicją operatora OR(|+) podaną przez Jasia wyżej.
Innymi słowy: odpowiedź Irbisola jest o pipce
3.
Pójście do kina i do teatru (K*T) jest warunkiem koniecznym ~> i wystarczającym => do tego, aby pójść do kina i do teatru (K*T)
K*T<=>K*T = (A1: K*T=>K*T)*(B1: K*T~>K*T)=1*1=1
Innymi słowy w AK mamy pewność absolutną że:
Każde pojęcie jest tożsame samo z sobą
p=p <=> (A1: p=>p)*(B1: p~>p) =1*1=1
Definicja znaczka =>:
p=>q = ~p+q
dla p=q mmay:
p=>p = ~p+p =1
Definicja znaczka ~>:
p~>q = p+~q
dla p=q mamy:
p~>p = p+~p=1
cnd
To jest powszechnie znana definicja równoważności p<=>q.
Dowód:
Klikamy na googlach:
„koniecznym i wystarczającym”
Wyników: 13 400
„potrzeba i wystarcza”
Wyników: 409 000!
Podobnych zdań prawdziwych na gruncie algebry Kubusia jest w stosunku do malunku z Wikipedii multum.
Powtórzmy istotę problemu.
Pani w I klasie LO:
Irbisolu, opowiedz nam o operatorze OR(|+) na podstawie zdania
ABC:
Jutro pójdziemy do kina lub do teatru
Odpowiedź Irbisola:
Operator OR(|+) to nie jest odpowiedź na dwa pytania:
1.
Kiedy jutro pani dotrzyma słowa
2.
Kiedy jutro pani skłamie
Jak to twierdzi głupi Jaś wyżej.
Irbisolowa definicja operatora OR(|+):
Operator OR(|+) mówi nam o warunkach wystarczających => i koniecznych ~> występujących w zdaniu ABC.
Pytanie do Irbisola:
Czy podtrzymujesz swoją definicję operatora OR(|+) wyżej?
Podsumowanie:
Jak wszyscy widzą, pani w I klasie LO pyta Irbisola o rybkę, czyli o definicję operatora OR(|+) a dostaje opowieść o pipce czyli o warunkach wystarczających => i koniecznych ~> występujących w zdaniu ABC
ABC:
Jutro pójdziemy do kina lub do teatru
Ostatnio zmieniony przez rafal3006 dnia Pią 11:43, 25 Mar 2022, w całości zmieniany 3 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Sob 14:12, 26 Mar 2022 Temat postu: Wysłany: Sob 14:12, 26 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#652939
Prawo rozbicia sumy logicznej zbiorów p+q!
Czy Irbisol zgodzi się na rzeczową dyskusję, bez epitetów?
| Irbisol napisał: | | rafal3006 napisał: | Nigdy nie stwierdziłem iż powyższy malunek poprawnie opisuje operator OR(|+).
Malunek z Wikipedii nie opisuje poprawnie operatora OR(|+) bo nie ma na mim zdarzenia/zbioru niepustego:
~(A+B)=~A*~B
zatem ten malunek jest czysto matematycznym fałszem w stosunku do operatora OR(|+) |
A skąd wiesz, że ów malunek w ogóle zamierzał opisywać OR? |
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych] |
W dalszej części wykładu robię podstawienie:
p=A
q=B
by być w zgodzie z powszechnie przyjętą logiką formalną (ogólną)
Po pierwsze:
Irbisolu, ten najpopularniejszy w ziemskiej logice matematycznej malunek (jak wyżej) prawidłowo pokazuje sumę logiczną zbiorów Y=p+q widzianą jako sumę logiczną trzech zbiorów rozłącznych wchodzących w skład tej sumy.
Innymi słowy:
Y=p+q - to pokazuje powyższy malunek
Zapis dokładnie tego samego w postaci trzech zbiorów niepustych i rozłącznych to:
Y = A: p*q + B: p*~q + C: ~p*q - to też doskonale widać na powyższym malunku
Minimalizujemy ostatni zapis:
Y = p*q + p*~q + ~p*q
Y = p*(q+~q)+~p*q - wyciągnięcie zmiennej p przed nawias
Y = p+(~p*q) - bo q+~q=1 oraz x*1=x
Przejście do logiki ujemnej (bo ~Y) poprzez negację zmiennych i wymianę spójników
~Y = ~p*(p+~q)
~Y = ~p*p + ~p*~q - wymnożenie wielomianu
~Y = ~p*~q - bo ~p*p=0 oraz 0+x=x
Powrót do logiki dodatniej poprzez negacje zmiennych i wymianę spójników
Y = p+q
Stąd mamy:
Założenie:
Zbiory p i q są niepuste, mają co najmniej jeden element wspólny i żaden z nich nie zawiera się w drugim.
To założenie spełnia powyższy malunek!
Prawo rozbicia sumy logicznej zbiorów p+q:
Dowolną sumę logiczną zbiorów p+q spełniającą powyższe założenie, można zapisać w postaci trzech zbiorów niepustych i rozłącznych uzupełniających się wzajemnie do sumy zbiorów p+q
p+q = A: p*q+ B: p*~q+ C: ~p*q
Pytanie do Irbisola:
Czy zgadzasz się z faktem, iż ziemska logika matematyczna nie zna kluczowego w logice matematycznej prawa rozbicia sumy logicznej zbiorów/zdarzeń p+q na trzy zbiory/zdarzenia niepuste i rozłączne jak niżej:
p+q = p*q+p*~q+~p*q
Diagram Venna:
[link widoczny dla zalogowanych]

Malunki z cytatu o diagramie Venna wyżej potwierdzają prawo rozbicia sumy logicznej p+q - czy zgadzasz się z tym faktem?
Ostatnio zmieniony przez rafal3006 dnia Sob 14:15, 26 Mar 2022, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Sob 19:42, 26 Mar 2022 Temat postu: Wysłany: Sob 19:42, 26 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#652983
Czy Irbisol nawiąże sensowną dyskusję?
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych] |
| Irbisol napisał: | | Nie odpowiedziałeś na pytanie. |
Na twoje pytanie odpowiedziałem precyzyjnie wyżej.
Powtórzę:
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#652905
| Irbisol napisał: | | rafal3006 napisał: | Nigdy nie stwierdziłem iż powyższy malunek poprawnie opisuje operator OR(|+).
Malunek z Wikipedii nie opisuje poprawnie operatora OR(|+) bo nie ma na mim zdarzenia/zbioru niepustego:
~(A+B)=~A*~B
zatem ten malunek jest czysto matematycznym fałszem w stosunku do operatora OR(|+) |
A skąd wiesz, że ów malunek w ogóle zamierzał opisywać OR? |
W dalszej części wykładu robię podstawienie:
p=A
q=B
by być w zgodzie z powszechnie przyjętą logiką formalną (ogólną)
Jedyną sensowną rzeczą jaką ów malunek opisuje poprawnie to prawo rozbicia sumy logicznej zbiorów p+q na trzy podzbiory niepuste i rozłączne:
p+q = A: p*q + B: p*~q + C: ~p*q
Poza tym jednym, sensownym opisem powyższy malunek jest totalnym dnem, czyli nie opisuje absolutnie niczego z zakresu logiki matematycznej tzn. nie masz szans na opisanie tym rysunkiem choćby jednego operatora logicznego.
W całej logice matematycznej jest 6 i tylko 6 operatorów jak niżej:
1. OR(|+)
##
2. AND(|*)
##
3. Operator implikacji prostej p||=>q
##
4. Operator implikacji odwrotnej p||~>q
##
5. Operator równoważności p|<=>q
##
5a. Operator "albo"(|$) - to jest szczególny przypadek równoważności:
p$q = p<=>~q = p*~q+~p*q
##
6. Operator chaosu p||~~>q
Gdzie:
## - różne na mocy definicji
Irbisolu, ja twierdzę że malunek z Wikipedii nie opisuje poprawnie ani jednego z powyższych operatorów, zatem z tego punktu widzenia jest jednym, wielkim, potwornie śmierdzącym gównem.
Jeśli twierdzisz, że nie jest gównem i ma jakiekolwiek zastosowanie w logice matematycznej, to pokaż to zastosowanie.
Poza oczywiście prawem rozbicia sumy logicznej na trzy rozłączne i niepuste zbiory, o którym to prawie (bardzo ważnym w logice) najwięksi ziemscy matematycy nie mają bladego pojęcia!
tzn. nie znajdziesz tego super ważnego prawa ani w Wikipedii ani w jakimkolwiek podręczniku logiki matematycznej.
P.S.
W kolejnym poście mogę ci udowodnić, że malunek z Wikipedii opisuje prawie dobrze operator implikacji prostej p||=>q, jednak „prawie” robi tu fundamentalną różnicę.
Czy przeczytasz?
Ostatnio zmieniony przez rafal3006 dnia Sob 19:58, 26 Mar 2022, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Sob 21:44, 26 Mar 2022 Temat postu: Wysłany: Sob 21:44, 26 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#653001
Czy Irbisol nawiąże sensowną dyskusję?
Czy Irbisol zgodzi się na króciutki wykład w temacie kiedy zdania podobne do tych z jego cytatu zaczną mieć sens, czyli zaczną opisywać operator implikacji prostej p||=>q albo odwrotnej p||~>q?
| Irbisol napisał: | | rafal3006 napisał: | | Cytat: | | A skąd wiesz, że ów malunek w ogóle zamierzał opisywać OR? |
W dalszej części wykładu robię podstawienie: |
Wiesz, że malunek miał opisywać, OR ponieważ ... < i tu dokończ zdanie > |
Malunek opisuje poprawnie tylko i wyłącznie spójnik "lub"(+) co udowodniłem w tym poście:
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#652939
Spójnik "lub"(+) jest częścią operatora OR(|+) ale to nie jest do samo co operator OR(|+)
Definicja operatora OR(|+)=operatora "lub"(|+)=(Y|=p+q):
Operator OR(|+)=(Y|=p+q) to układ równań logicznych 1 i 2 dający odpowiedź na pytanie o Y i ~Y:
1.
Y=p+q
co w logice jedynek oznacza:
Y=1 <=> p=1 lub q=1
.. a kiedy zajdzie ~Y)
Negujemy równanie 1 stronami:
~Y=~(p+q)=~p*~q
stąd mamy:
2.
~Y=~p*~q
co w logice jedynek oznacza:
~Y=1 <=> ~p=1 i ~q=1
Czy to jest dla ciebie zrozumiałe?
tzn. czy widzisz różnicę między operatorem "lub"(|+) a spójnikiem "lub"(+)?
Jeśli powiesz tak, to przejdziemy do duuużo ciekawszych rzeczy, gdzie zdania w cytacie niżej zaczną mieć sens.

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych]
Ostatnio zmieniony przez rafal3006 dnia Nie 7:29, 27 Mar 2022, w całości zmieniany 3 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Nie 13:07, 27 Mar 2022 Temat postu: Wysłany: Nie 13:07, 27 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#653105
Czy Irbisol nawiąże sensowną dyskusję?
Czy Irbisol zgodzi się na króciutki wykład w temacie kiedy zdania podobne do tych z jego cytatu zaczną mieć sens, czyli zaczną opisywać operator implikacji prostej p||=>q albo odwrotnej p||~>q?
| Irbisol napisał: | | Nadal nie wiem, skąd ci przyszło do głowy, że malunek ma opisywać OR. |
Jak wszyscy widzą, Irbisola w ogóle nie interesuje dyskusja na temat JEGO malunku z Wikipedii!
Irbisol będzie teraz do końca świata powtarzał to zdanie wyżej, mimo iż napisałem mu w moich postach wyżej, że malunek z angielskiej Wikipedii nie pasuje do żadnego z sześciu możliwych operatorów logicznych - oczywiście wszystko mogę po kolei udowodnić.
Na razie zajmujemy się operatorem OR(|+)
Malunek z angielskiej Wikipedii przytoczony przez Irbisola jest następujący:
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych] |
Irbisolu,
W moich postach wyżej napisałem ci, że rysunek z Wikipedii nie spełnia definicji żadnego z możliwych operatorów logicznych, w tym operatora OR(|+).
Po raz kolejny zajmę się w niniejszym poście operatorem OR(|+).
Podstawiam:
p=A
q=B
aby być w zgodzie z zapisem ogólnym w logice matematycznej.
Do poprawnego opisu operatora OR(|+) powyższemu malunkowi brakuje straszliwie dużo bowiem nie chodzi tu tylko uzupełnienie zbioru p+q do wspólnej dziedziny D w postaci zbioru ~(p+q)=~p*~q
Przede wszystkim brakuje na nim logiki dodatniej (bo Y):
Y=p+q
oraz logiki ujemnej (bo ~Y):
~Y=~p*~q
Poprawny diagram operatora OR(|+) wraz z objaśnieniami jest w tym fragmencie algebry Kubusia
http://www.sfinia.fora.pl/forum-kubusia,12/algebra-kubusia-matematyka-jezyka-potocznego-w-trakcie,20453.html#641805
4.1 Operator A1: Y|=p+q wyrażony spójnikami „i”(*) i „lub”(+)
Częstotliwość użycia w języku potocznym: bardzo duża
Definicja matematyczna operatora A1: Y|=p+q w spójnikach „i”(*) i „lub”(+):
Definicja matematyczna operatora A1: Y|=p+q wyrażonego spójnikami „i”(*) i „lub”(+) jest spełniona wtedy i tylko wtedy gdy wszystkie możliwe człony funkcji logicznej Y i ~Y przyjmują wartość logiczną 1.
Definicja fizyczna operatora Y|=p+q w spójnikach „i”(*) i „lub”(+):
Definicja fizyczna operatora Y|=p+q wyrażonego spójnikami „i”(*) i „lub”(+) jest spełniona wtedy i tylko wtedy gdy iloczyny logiczne zdarzeń/zbiorów p i q przez wszystkie możliwe przeczenia p i q będą zdarzeniami możliwymi ~~> lub zbiorami niepustymi ~~>.
Innymi słowy:
Definicja fizyczna operatora Y|=p+q wyrażonego spójnikami „i”(*) i „lub”(+) jest spełniona wtedy i tylko wtedy gdy na mocy teorii zbiorów/zdarzeń nie da się zredukować ani funkcji logicznej Y ani też funkcji logicznej ~Y
Definicja matematyczna operatora Y|=p+q to układ równań logicznych 1 i 2 dający odpowiedź na pytanie o Y i ~Y:
1.
Y=p+q
co w logice jedynek oznacza:
Y=1 <=> p=1 lub q=1
.. a kiedy zajdzie ~Y?
Negujemy równanie 1 stronami:
2.
~Y=~p*~q
co w logice jedynek oznacza:
~Y=1 <=> ~p=1 i ~q=1
Definicja spójnika „lub”(+) w zdarzeniach/zbiorach rozłącznych:
p+q = p*q + p*~q + ~p*q
Stąd mamy tożsamą funkcję logiczną Y w logice dodatniej (bo Y):
1’
Y = A: p*q+ B: p*~q + C: ~p*q
Dowód:
Minimalizujemy funkcję 1’:
Y = p*q + p*~q + ~p*q
Y = p*(q+~q)+~p*q
Y = p+(~p*q)
Przejście do logiki ujemnej (bo ~Y) poprzez negację zmiennych i wymianę spójników:
~Y = ~p*(p+~q)
~Y = ~p*p+~p*~q
~Y=~p*~q
Powrót do logiki dodatniej (bo Y) poprzez negację zmiennych i wymianę spójników:
Y = p+q
cnd
Stąd mamy:
1: Y=p+q [=] 1’: Y = A: p*q+ B: p*~q + C: ~p*q
Diagram w zdarzeniach opisujący ten przypadek jest następujący:
| Kod: |
D1
Definicja operatora A1: Y|=p+q w zdarzeniach
--------------------------------------------------------------------------
| D=p*q+p*~q+~p*q+~p*~q=1 - dziedzina, suma logiczna zdarzeń rozłącznych |
--------------------------------------------------------------------------
| p |
------------------------------------------------------
| q |
--------------------------------------------------------------------------
| B: Yb=p*~q | A: Ya=p*q | C: Yc=~p*q | D:~Yd=~p*~q |
--------------------------------------------------------------------------
|
Zdarzenia ABCD to zdarzenia niepuste i rozłączne uzupełniające się wzajemnie do dziedziny D
Dowód wzajemnej rozłączności zdarzeń ABCD:
A: p*q
B: p*~q
C: ~p*q
D: ~p*~q
Mnożymy logicznie każde zdarzenie z każdym:
A*B=(p*q)*(p*~q)=[] =0 - bo q*~q=0
A*C=(p*q)*(~p*q)=[] =0 - bo p*~p=0
A*D=(p*q)*(~p*~q)=[]=0 - bo p*~p=0
B*C=(p*~q)*(~p*q)=[]=0 - bo p*~p=0
B*D=(p*~q)*(~p*~q)=[]=0 - bo p*~p=0
C*D=(~p*q)*(~p*~q)=[]=0 - bo q*~q=[]=0
cnd
Dowód iż zdarzenia ABCD uzupełniają się wzajemnie do dziedziny D:
D = A: p*q + B: p*~q + C: ~p*q + D: ~p*~q
D=p*q + p*~q + ~p*q + ~p*~q
D=p*(q+~q) + ~p*(q+~q)
D=p+~p =1
cnd
Uważaj teraz Irbisolu!
Najsłynniejszemu malunkowi z ziemskich podręczników matematyki brakuje też FUNDAMENTU, dzięki któremu mamy 100% przełożenie teorii zbiorów na logikę matematyczną.
Ten fundament to przede wszystkim przypisanie zbiorom wartości logicznych:
[]=0 - zbiór pusty, nie zawierający choćby jednego pojęcia zrozumiałego dla człowieka
[samochód, krasnoludek, miłość .. ]=1 - zbiór niepusty, zawierający co najmniej jedno pojęcie zrozumiałe dla człowieka
Pełny wykład na temat FUNDAMENTALNYCH różnic w teorii zbiorów między algebrą Kubusia a jakąkolwiek logiką matematyczną ziemian znajdziemy w algebrze Kubusia.
http://www.sfinia.fora.pl/forum-kubusia,12/algebra-kubusia-matematyka-jezyka-potocznego-w-trakcie,20453.html#648077
5.2 Definicje podstawowe w Kubusiowej teorii zbiorów
Przypomnijmy znane już definicje podstawowe.
Definicja pojęcia:
Pojęcie to wyrażenie zrozumiałe dla człowieka
Przykłady pojęć zrozumiałych:
p = [pies, miłość, krasnoludek, ZWZ, LN ...]
Przykłady pojęć niezrozumiałych:
q = [agstd, sdked …]
Pojęcia mają wartości logiczne:
1 = prawda, gdy pojęcie jest zrozumiałe (np. pies)
0 = fałsz, gdy pojęcie jest niezrozumiale (np. agstd)
Prawo Rekina:
Żaden człowiek nie posługuje się w języku potocznym pojęciami których nie rozumie
Definicja elementu zbioru:
Element zbioru to dowolne pojęcie zrozumiałe przez człowieka, które umieści w swoim zbiorze
Definicja zbioru:
Zbiór to zestaw dowolnych pojęć zrozumiałych dla człowieka
Zauważmy, że w definicji zbioru nie ma zastrzeżenia, iż elementem zbioru nie może być podzbiór, czy też zbiór.
Definicja Uniwersum:
Uniwersum to zbiór wszelkich pojęć zrozumiałych dla człowieka.
Czyli:
U = [pies, miłość, krasnoludek ...] - wyłącznie pojęcia rozumiane przez człowieka (zdefiniowane)
Uniwersum człowieka jest dynamiczne tzn. rozszerza się gdy się uczymy (poznajemy nowe pojęcia) i zawęża gdy zapominamy wyuczonych kiedyś pojęć. Na mocy definicji w żadnym momencie nie możemy wyjść poza swoje, indywidualne Uniwersum.
Zauważmy, że zaledwie 40 lat temu pojęcie „Internet” było zbiorem pustym, nie istniało - ale w dniu dzisiejszym już tak nie jest, Uniwersum ludzkości rozszerzyło się o to pojęcie, znane praktycznie każdemu człowiekowi na Ziemi.
Podobnie będzie z algebrą Kubusia, aktualnie wyłącznie mieszkańcy 100-milowego lasu ją znają i rozumieją, ale wkrótce pojęcie „Algebra Kubusia” znane będzie każdemu ziemianinowi od 5-cio latka poczynając, bowiem algebra Kubusia będzie uczona we wszystkich ziemskich przedszkolach - oczywiście w formie zabawy praktycznej, bez teorii którą znają wszystkie żywe stworzenia, nie będąc tego świadomym.
Definicja zbioru pustego []:
Zbiór pusty to zbiór zawierający zero pojęć zrozumiałych dla człowieka
Czyli:
[] = [agstd, sdked …] - wyłącznie pojęcia niezrozumiałe dla człowieka (jeszcze niezdefiniowane)
Definicja dziedziny absolutnej DA:
Dziedzina absolutna DA to zbiór wszelkich pojęć możliwych do zdefiniowania w naszym Wszechświecie.
Zbiór wszystkich zbiorów:
Zbiór wszystkich zbiorów jest tożsamy z dziedziną absolutną DA.
Definicja Uniwersum:
Uniwersum U to zbiór wszelkich pojęć zrozumiałych dla człowieka.
Definicja zbioru pustego []:
Zbiór pusty [] to zbiór zawierający zero pojęć zrozumiałych dla człowieka.
Zbiór pusty zawiera nieskończenie wiele pojęć niezrozumiałych dla człowieka, jeszcze nie zdefiniowanych. Definiować elementy w naszym Wszechświecie może wyłącznie człowiek, świat martwy sam sobie nic nie definiuje.
Przed pojawieniem się człowieka na ziemi zawartość zbioru pustego była taka:
[] - wszystkie elementy naszego Wszechświata w sensie absolutnym, nie ma jeszcze człowieka który by cokolwiek definiował.
W dniu dzisiejszym sytuacja jest inna, taka:
| Kod: |
T1
Algebra Kubusia:
-------------------------------------------------------------------
| Zbiór pusty [] | Uniwersum U |
| Pojęcia jeszcze przez człowieka | Pojęcia przez człowieka już |
| niezdefiniowane | zdefiniowane |
| Niezrozumiałe dla człowieka | Zrozumiałe dla człowieka |
| | |
-------------------------------------------------------------------
| DA - dziedzina absolutna |
-------------------------------------------------------------------
|
Na mocy powyższego zachodzi:
[] = ~U - zbiór pusty [] to zaprzeczenie Uniwersum U w dziedzinie absolutnej DA
U = ~[] - zbiór Uniwersum U to zaprzeczenie zbioru pustego [] w dziedzinie absolutnej DA
Na mocy definicji dziedziny absolutnej mamy:
1: U+~U = U+[] =U =1
2: U*~U = U*[] =[] =0
Komentarz:
1.
Do zbioru Uniwersum (pojęcia zrozumiałe dla człowieka) możemy dodać elementy ze zbioru ~U (pojęcia niezrozumiałe dla człowieka), ale na mocy definicji Uniwersum wszelkie elementy ze zbioru ~U=[] musimy natychmiast usunąć, inaczej gwałcimy definicję Uniwersum.
2.
U*~U=[] =0
Iloczyn logiczny elementów ze zbioru U (pojęcia zrozumiałe dla człowieka) i ~U (pojęcia niezrozumiałe dla człowieka) jest zbiorem pustym tzn. nie ma ani jednego elementu wspólnego w zbiorach U i ~U=[].
Prawo Owieczki:
Prawdziwe jest zdanie ziemskich matematyków iż „ze zbioru pustego [] wynika wszystko” wtedy i tylko wtedy gdy definicje zbioru pustego [] i Uniwersum U będą zgodne z definicjami obowiązującymi w algebrze Kubusia.
Ostatnio zmieniony przez rafal3006 dnia Nie 13:13, 27 Mar 2022, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Nie 15:31, 27 Mar 2022 Temat postu: Wysłany: Nie 15:31, 27 Mar 2022 Temat postu: |
|
|
Ostatnie tchnienie wstępu co algebry Kubusia!
Właśnie doszedłem do wniosku, że wstęp do algebry Kubusia jest zdecydowanie za długi, w finalnej wersji zostawię około 5-10% tego co niżej.
Algebra Kubusia - matematyka języka potocznego
W trakcie pisania
2022-03-09
Powstaje najnowsza wersja algebry Kubusia, zminimalizowana do najważniejszych definicji i praw algebry Kubusia.
Autor:
Kubuś ze 100-milowego lasu
Rozszyfrowali:
Rafal3006 i przyjaciele
Dziękuję wszystkim, którzy dyskutując z Rafałem3006 przyczynili się do odkrycia algebry Kubusia (cytuję w kolejności zaistnienia):
Wuj Zbój, Miki (vel Lucek), Volrath, Macjan, Irbisol, Makaron czterojajeczny, Quebab, Windziarz, Fizyk, Idiota, Sogors (vel Dagger), Fiklit, Yorgin, Pan Barycki, Zbigniewmiller, Mar3x, Wookie, Prosiak, Andy72, Michał Dyszyński, Szaryobywatel, Jan Lewandowski, MaluśnaOwieczka i inni.
Kluczowi przyjaciele Kubusia, dzięki którym algebra Kubusia została rozszyfrowana to (cytuję w kolejności zaistnienia):
1.
Rafał3006
2.
Wuj Zbój - dzięki któremu Rafal3006 poznał istotę implikacji od strony czysto matematycznej.
3.
Fiklit - który poświęcił 8 lat życia na cierpliwe tłumaczenie Rafałowi3006 jak wygląda otaczający nas świat z punktu widzenia Klasycznego Rachunku Zdań
Bez Fiklita o rozszyfrowaniu algebry Kubusia moglibyśmy wyłącznie pomarzyć
4.
Irbisol - znakomity tester końcowej wersji algebry Kubusia, za wszelką cenę usiłujący ją obalić.
Czyż można sobie wymarzyć lepszego testera?
5.
MaluśnaOwieczka - końcowy uczestnik dyskusji o algebrze Kubusia w trakcie której wiele definicji zostało doprecyzowanych.
Niniejszy podręcznik jest końcowym efektem 16-letniej dyskusji na forach śfinia, ateista.pl i yrizona - to około 30 tys postów, średnio 5 postów dziennie wyłącznie na temat logiki matematycznej.

Spis treści:
1.0 Operatory jednoargumentowe
2.0 Podstawowa algebra Boole’a
2.7 Geneza błędu czysto matematycznego prof. L. Newelskiego
3.0 Dwuargumentowe funkcje logiczne
4.0 Operatory Y|=f(x) z grupy TF0-TF3 wyrażone spójnikami „i”(*) i „lub”(+)
5.0 Kubusiowa teoria zbiorów
6.0 Fundamenty obsługi zdań warunkowych w algebrze Kubusia
7.0 Spójniki obsługujące zdania warunkowe „Jeśli p to q”
8.0 Implikacja prosta p|=>q i odwrotna p|~>q
8.1 Implikacja prosta p|=>q w logice dodatniej (bo q)
8.4 Implikacja odwrotna p|~>q w logice dodatniej (bo q)
8.7 Implikacja prosta p|=>q vs implikacja odwrotna p|~>q
8.9 Geneza tabel zero-jedynkowych warunku wystarczającego => i koniecznego ~>
9.0 Spójniki równoważności p<=>q i „albo”($) p$q
9.1 Równoważność p<=>q w zbiorach
9.4 Równoważność p<=>q w zdarzeniach
9.5 Przykłady równoważności w zbiorach TP<=>SK i zdarzeniach A<=>S
Wstęp:
Przez ostatnie 16 lat intensywnie pracowałem (30 000 postów) nad „Algebrą Kubusia”, logiką matematyczną, pod którą podlega cały nasz Wszechświat żywy i martwy (w tym matematyka). Formalnie algebry Kubusia nie musimy się uczyć bo po prostu pod nią polegamy nie mając żadnych szans, aby się od niej uwolnić. Wynika z tego, że ekspertem algebry Kubusia jest każdy człowiek (od 5-cio latka poczynając) tylko póki co, o tym nie wie.
Algebra Kubusia to również podłożenie matematyki pod język potoczny człowieka, czyli coś, o czym matematycy marzą od 2500 lat (od Sokratesa).
Po co komu algebra Kubusia skoro wszyscy jesteśmy jej ekspertami?
Pytanie analogiczne to:
Po co komu znajomość gramatyki języka polskiego, skoro 5-cio latek biegle posługuje się językiem ojczystym nie znając formalnej gramatyki języka?
Osobiście nigdy nie znałem i nie znam formalnej gramatyki języka polskiego tzn. nie wiem co to jest jakiś tam podmiot, orzeczenie, przysłówek etc. … a po polsku potrafię pisać.
Mam nadzieję, że koniec końców ziemscy matematycy zaakceptują algebrę Kubusia jako jedyną poprawną logikę matematyczną obowiązującą w naszym Wszechświecie.
Czy ziemscy matematycy okażą się matematycznymi tłukami?
Tak, jeśli nie zrozumieją algebry Kubusia, logiki matematycznej pod którą sami podlegają!
Pewne jest, że wcześniej czy później 100% matematyków przejdzie do obozu algebry Kubusia, wyrzucając na śmietnik logikę matematyczną zwaną „Klasycznym Rachunkiem Zdań”
Uzasadnienie:
[link widoczny dla zalogowanych]
| Wikipedia napisał: | Kiedy odkryto liczby ujemne?
Czy liczb ujemnych używano tak samo wcześnie jak liczb dodatnich? Nie! To zaskakujące, że liczby ujemne znamy od całkiem niedawna (szczególnie w Europie), a pełne zasady arytmetyki opracowano dopiero na początku XIX wieku.
Liczby ujemne stosowano od bardzo dawna dla określenia długu. Pierwsza wzmianka o liczbach ujemnych pojawia się w okresie II w. p.n.e. - I w. n.e. w Chinach w dziele wielu autorów w Matematyce w dziewięciu księgach - Jiuzhang suanshu. |
Algebra Kubusia to między innymi odkrycie logiki dodatniej (bo Y) i ujemnej (bo ~Y) w logice matematycznej, to jest co innego niż znana ziemianom logika dodatnia i ujemna w sprzęcie (bramkach logicznych).
[link widoczny dla zalogowanych]
| Wikipedia napisał: |
W układach logicznych, gdzie są zdefiniowane tylko dwie wartości liczbowe, rozróżnia się dwa przedziały napięć: wysoki (ozn. H, z ang. high) i niski (ozn. L, z ang. low); pomiędzy nimi jest przerwa, dla której nie określa się wartości liczbowej – jeśli napięcie przyjmie wartość z tego przedziału, to stan logiczny układu jest nieokreślony.
Jeśli do napięć wysokich zostanie przyporządkowana logiczna jedynka, a do niskich logiczne zero, wówczas mówi się, że układ pracuje w logice dodatniej (inaczej zwanej pozytywną), w przeciwnym razie mamy do czynienia z logiką ujemną (lub negatywną). |
Teraz proszę o uwagę:
Jeśli znana jest ziemianom logika dodatnia i ujemna na poziomie sprzętu (jak wyżej) to musi istnieć logika dodatnia (bo Y) i ujemna (bo ~Y) na poziomie logiki matematycznej.
Definicja logiki dodatniej (bo Y) i ujemnej (bo ~Y) w logice matematycznej:
Zmienna binarna Y zapisana jest w logice dodatniej (bo Y) wtedy i tylko wtedy gdy nie jest zaprzeczona
Zmienna binarna Y zapisana jest w logice ujemnej (bo ~Y) wtedy i tylko wtedy gdy jest zaprzeczona (~).
Podsumowując:
Jeśli ziemscy matematycy okażą się matematycznymi tłukami to ich akceptacja logiki dodatniej (bo Y) i ujemnej (bo ~Y) w logice matematycznej może trwać tyle, co akceptacja przez europejskich matematyków liczb ujemnych w matematyce, czyli około 2000 lat.
W dobie Internetu na akceptację algebry Kubusia nie będziemy tyle czekać przede wszystkim dlatego, że wszyscy jesteśmy ekspertami algebry Kubusia, od 5-cio latka poczynając!
Część I „Algebry Kubusia”
Część I „Algebry Kubusia” (do punktu 4.0) to nawiązanie do logiki matematycznej zwanej „Algebrą Boole’a”.
Algebra Kubusia to matematyczny opis języka potocznego, zatem tylko z tego punktu widzenia będziemy patrzeć na algebrę Boole’a.
Algebra Boole’a operuje na zaledwie 5 znaczkach:
1 - prawda
0 - fałsz
(~) - negacja
„i”(*) - spójnik „i”(*) z języka potocznego
„lub”(+) - spójnik „lub”(+) z języka potocznego
Wszystko co jest ponad to, nie jest algebrą Boole’a.
Algebra Kubusia zawiera w sobie algebrę Boole’a mówiącą wyłącznie o spójnikach „i”(*) i „lub”(+) z języka potocznego człowieka.
Innymi słowy:
Algebra Boole’a w ogóle nie zajmuje się kluczową i najważniejszą częścią logiki matematycznej, czyli obsługą zdań warunkowych „Jeśli p to q”.
Błędy fatalne w aktualnej algebrze Boole’a:
1.
Klasyczna algebra Boole’a nie zna kluczowych dla logiki matematycznej pojęć: logika dodatnia (bo Y) i logika ujemna (bo ~Y)
2.
Ziemski rachunek zero-jedynkowy (fundament logiki matematycznej) jest wewnętrznie sprzeczny na poziomie funkcji logicznych Y i ~Y (prawo Grzechotnika)
Największą tragedią ziemskiej logiki matematycznej jest fakt, że w bramkach logicznych po stronie wejścia cyfrowego widzi ona zmienne binarne w logice dodatniej (bo p) i ujemnej (bo ~p), ale nie widzi dokładnie tego samego po stronie wyjścia cyfrowego Y, tu obowiązuje bezwzględny zakaz widzenia wyjścia Y w logice ujemnej (bo ~Y).
Odpowiednikiem tego faktu w matematyce klasycznej byłoby widzenie w układzie Kartezjańskim na osi X zmiennych dodatnich (x) i zmiennych ujemnych (~x) z zakazem widzenia dokładnie tego samego na osi Y, gdzie dozwolone byłoby widzenie jedynie zmiennych dodatnich (y).
Czy ktokolwiek wyobraża sobie współczesną matematykę z takim upośledzonym układem Kartezjańskim?
Film powinien zaczynać się od trzęsienia ziemi, potem zaś napięcie ma nieprzerwanie rosnąć
Alfred Hitchcock.
Prawo Grzechotnika:
Ziemski rachunek zero-jedynkowy który nie widzi funkcji logicznej w logice dodatniej (bo Y) i funkcji logicznej w logice ujemnej (bo ~Y) jest wewnętrznie sprzeczny na poziomie funkcji logicznych.
Dowód w punkcie 1.2.1 oraz 3.1
Część II „Algebry Kubusia”
Część II „Algebry Kubusia” (od punktu 5.0) to właściwa algebra Kubusia, czyli matematyczna obsługa wszelkich zdań warunkowych „Jeśli p to q” totalnie nieznana ziemskim matematykom.
Niniejsza wersja algebry Kubusia to minimalistyczny zapis definicji i praw algebry Kubusia konieczny i wystarczający dla jej zrozumienia, to kręgosłup algebry Kubusia.
Wiele aspektów algebry Kubusia zostało tu pomiętych jako nieistotnych dla zrozumienia idei algebry Kubusia - można je znaleźć w starszych wersjach AK.
Dlaczego logika matematyczna zwana „Klasycznym Rachunkiem Zdań” jest do bani?
Jeden z wielu przykładów:
W ziemskiej logice matematycznej zwanej „Klasycznym Rachunkiem Zdań” funkcjonuje prawo eliminacji implikacji:
p=>q = ~p+q
W praktyce języka potocznego żaden człowiek, od 5-cio latka poczynając na najwybitniejszym matematyku kończąc nigdy tego prawa nie używa, bowiem jego użycie to zabicie istoty zdań warunkowych „Jeśli p to q”, czyli zabicie warunków wystarczających => i koniecznych ~> definiowanych zdaniami warunkowymi „Jeśli p to q”
Przykład:
A1.
Jeśli jutro będzie padało (P) to na 100% => będzie pochmurno (CH)
P=>CH=1
Padanie jest warunkiem wystarczającym => do tego, aby było pochmurno bo zawsze gdy pada, są chmury.
Padanie daje nam gwarancję matematyczną => istnienia chmur, bo padać może wyłącznie z chmury.
Zachodzi tożsamość pojęć:
Warunek wystarczający => = Gwarancja matematyczna =>
Prawo eliminacji implikacji z ziemskiej logiki matematycznej:
A1: P=>CH = ~P+CH
Prawa strona generuje nam zdanie twierdzące zawsze prawdziwe:
G1.
Jutro nie będzie padało (~P) lub będzie pochmurno (CH)
Y = ~P+CH
Dowód iż jest to zdanie zawsze prawdziwe:
Definicja spójnika „lub”(+) w zdarzeniach/zbiorach rozłącznych:
p+q = p*q+p*~q+~p*q
Podstawiając nasz przykład mamy:
Y = ~P+CH = ~P*CH + ~P*~CH + P*CH
Czyli:
Y = A: P*CH + C:~P*~CH + D: ~P*CH
Gdzie:
Y = Ya+Yc+Yd - funkcja logiczna Y jest sumą logiczną funkcji cząstkowych {Ya, Yc, Yd}
W rozbiciu na zdarzenia cząstkowe mamy:
A:
Ya=P*CH=1*1=1
Możliwe jest (=1) zdarzenie (Ya): pada (P) i jest pochmurno (CH)
cnd
C:
Yc=~P*~CH=1*1=1
Możliwe jest (=1) zdarzenie (Yc): nie pada (~P) i nie jest pochmurno (~CH)
cnd
D:
Yd=~P*CH=1*1=1
Możliwe jest (=1) zdarzenie (Yd): nie pada (~P) i jest pochmurno (CH)
cnd
Zauważmy, że ostatnie możliwe zdarzenie rozłączne jest zdarzeniem pustym:
Yb=P*~CH=1*1=[] =0
Niemożliwe jest (=0) zdarzenie (Yb): pada (P) i nie jest pochmurno (~CH)
cnd
Dokładnie dlatego zdanie głupoty G1, zabijające warunek wystarczający => w zdaniu A1: P=>CH jest zdaniem zawsze prawdziwym
cnd
Historia wynalazków naukowych i technicznych uczy nas, że rasa ludzka uboga jest w niezależną myśl twórczą i wyobraźnię... człowiek musi niejako dosłownie potknąć się o rzecz samą, aby mu zakwitła Idea.
Albert Einstein
Ten wytłuszczony fragment to święta prawda.
Moje potknięcie nastąpiło zupełnie przypadkowo 26 lat po skończeniu studiów elektronicznych na forum śfinia, gdzie zaskoczony zostałem zdaniami prawdziwymi w ziemskiej logice „matematycznej” zwanej „Klasycznym Rachunkiem Zdań” typu:
Jeśli 2+2=5 to 2+2=4
Jeśli 2+2=4 to Płock leży nad Wisłą
Jeśli 2+2=5 to jestem Papieżem
Dowód na serio prawdziwości ostatniego zdania w logice matematycznej ziemskich matematyków jest następujący:
[link widoczny dla zalogowanych]
| Wikipedia napisał: |
Matryca implikacji od wieków budzi kontrowersje, niekiedy sięgające samej istoty logiki.
Matryca implikacji:
| Kod: |
p q p=>q
1 1 1
0 1 1
1 0 0
0 0 1
|
Z dowolnego zdania fałszywego wynika dowolne zdanie prawdziwe (drugi wiersz matrycy) i dowolne zdanie fałszywe (czwarty wiersz matrycy). Twierdzenie to znane jest od wielu wieków w postaci łacińskiej formuły Falsum sequitur quodlibet (z fałszu wynika cokolwiek, czyli wszystko).
Mimo to, gdy Bertrand Russell opublikował swój system logiki oparty na omawianej matrycy implikacji materialnej, niektórzy filozofowie przyjęli ten system za rodzaj herezji logicznej.
Ktoś próbował wykpić B. Russella, ogłaszając list otwarty, w którym zaproponował mu do rozwiązania następujące zadanie:
Ponieważ według pana można udowodnić wszystko na podstawie jednego zdania fałszywego, proszę na podstawie fałszywego zdania "5 = 4" udowodnić, że jest pan papieżem.
Na pierwszy rzut oka zadanie to może się wydać niewykonalne. Intuicyjnie bowiem nie potrafimy dojrzeć żadnego związku między zdaniem "5 = 4" a zdaniem: "B. Russell jest papieżem". Intuicji nie można jednak wierzyć ślepo, jest bowiem zawodna. Russell podjął zadanie i rozwiązał je w wyniku następującego rozumowania:
Opierając się na regule głoszącej, że od obu stron równości wolno odjąć tę samą liczbę, odejmuję od obu stron równości: "5 = 4", liczbę 3. Wyprowadzam w ten sposób ze zdania "5 = 4" zdanie "2 = 1".
Dowód, że jestem papieżem, jest już teraz zupełnie prosty: papież i ja to dwie osoby, ale 2 = 1 (w tym przypadku papież i B. Russell, czyli dwie osoby są jedną osobą), więc jestem papieżem.
Rozumowanie to jest zupełnie poprawne, zatem początkowa intuicja zgodnie z którą zadanie dane Russellowi wydawało się nierozwiązalne, okazała się zawodna.
Zdanie "B. Russell jest papieżem" rzeczywiście wynika ze zdania "5 = 4". Jest to przykład wynikania fałszu z fałszu (odpowiednik czwartego wiersza matrycy).
Równie łatwo możemy wykazać, że z tego samego zdania fałszywego wynika zdanie prawdziwe, np. zdanie "B. Russell jest wykształcony". Wystarczy do już wyprowadzonego zdania "B. Russell jest papieżem" dodać oczywiście prawdziwe zdanie "Każdy papież jest wykształcony" i mamy:
B. Russell jest papieżem
Każdy papież jest wykształcony
zatem B. Russell jest wykształcony
Można również łatwo wskazać inne, prawdziwe konsekwencje zdania "5 = 4", np. "B. Russell jest mężczyzną", "B. Russell zna język łaciński", B. Russell jest osobistością znaną w całym świecie" itp.
Teoretyczna możliwość wyprowadzenia dowolnego zdania z danego zdania fałszywego nie zawsze jest równoznaczna z praktyczna łatwością wykonania takiego zadania. Ale takie zadanie jest do rozwiązania. |
… a tu bloger Gżdacz potwornie szydzi (i słusznie) z logiki „matematycznej” ziemskich matematyków:
[link widoczny dla zalogowanych]
| Gżdacz w artykule wynurzenia z szamba napisał: |
Jeśli 2+2=5, to jestem papieżem
Z książki Johna D. Barrowa Kres możliwości? wypisuję cytaty, które są cytatami drugiego rzędu, bo w rzeczonej książce są to również cytaty.
Cytat pierwszy (s. 226).
Sądzę, że mistycyzm można scharakteryzować jako badanie tych propozycji, które są równoważne swoim zaprzeczeniom. Z zachodniego punktu widzenia, klasa takich propozycji jest pusta. Ze wschodniego punktu widzenia klasa ta jest pusta wtedy i tylko wtedy, kiedy nie jest pusta. (Raymond Smullyan)
Przepisałem wiernie, pozostawiając niepoprawną interpunkcję oraz nadużycie leksykalne polegające na tłumaczeniu angielskiego proposition jako propozycja, zamiast stwierdzenie.
Cytat drugi (s. 226) wymaga lekkiego wprowadzenia.
Warunkiem niesprzeczności systemu w logice klasycznej jest ścisły podział zdań na prawdziwe bądź fałszywe, bowiem ze zdania fałszywego można wywnioskować dowolne inne, fałszywe bądź prawdziwe.
Kiedy Bertrand Russell wypowiedział ten warunek na jednym z publicznych wykładów jakiś sceptyczny złośliwiec poprosił go, by udowodnił, że jeśli 2 razy 2 jest 5, to osoba pytająca jest Papieżem. Russell odparł: "Jeśli 2 razy 2 jest 5, to 4 jest 5; odejmujemy stronami 3 i wówczas 1=2. A że pan i Papież to 2, więc pan i Papież jesteście jednym."!
W ramach zadania domowego zadałem sobie wykazanie, że jeśli Napoleon Bonaparte był kobietą, to ja jestem jego ciotką. Na razie zgłaszam "bz".
|
W roku 1980 ukończyłem wydział elektroniki na Politechnice Warszawskiej. Z racji wykształcenia byłem naturalnym ekspertem algebry Boole’a która w owym czasie była dla mnie najświętszą prawdą.
Na I roku elektroniki jest laboratorium bramek logicznych gdzie w naturalnej logice matematycznej człowieka opisywaliśmy jak zadany układ ma działać. Przełożenie takiego opisu na bramki logiczne było w skali 1:1 tzn. wszędzie tam gdzie w naturalnej logice człowieka użyliśmy spójnika „lub”(+) stosowaliśmy bramkę OR(+) zaś tam gdzie użyty był spójnik „i”(*) waliliśmy bramkę AND(*), ot i cała tajemnica projektowania dowolnego układu sterującego w bramkach logicznych.
W ten sposób w naturalnej logice matematycznej człowieka tworzyliśmy funkcję algebry Boole’a Y=f(x) opisującą sterowany układ.
Funkcja logiczna złożonego układu z reguły nie była minimalna. Warunkiem zaliczenia ćwiczenia było zminimalizowanie układu, walka z wyścigami i hazardem (możliwymi do wystąpienia w bramkach logicznych) oraz zaprezentowanie działającego urządzenia.
O co w tym wszystkim chodzi, najlepiej pokazać na przykładzie udając się do przedszkola, gdzie 5-cio letni eksperci algebry Kubusia zademonstrują nam, jak tworzy się poprawne sterowanie windą.
Rozważmy projektowanie sterowania windą.
Przyjmijmy wejście układu windy:
Na poziomie 5-cio latka zakładamy że winda ma dwa przyciski wejściowe układu (zmienne binarne):
Opis przycisku D=[drzwi]:
D=1 - drzwi zamknięte (D)
~D=1 - drzwi nie zamknięte (~D)
Opis przycisku P=[piętro]:
P=1 - przycisk piętro wciśnięty (P)
~P=1 - przycisk piętro nie wciśnięty (~P)
Przyjmijmy wyjście układu windy:
Wyjście układu opisane jest przez zmienną binarną J=[jedzie]:
J=1 - winda jedzie (J).
~J=1 - winda nie jedzie (~J)
I.
Pani przedszkolanka do Jasia (lat 5):
Powiedz nam Jasiu kiedy winda jedzie (J=1)?
Jaś:
A1.
Winda jedzie (J=1) wtedy i tylko wtedy gdy drzwi są zamknięte (D=1) i wciśnięty jest przycisk piętro (P=1)
A1: J=D*P
co w logice jedynek oznacza:
J=1 <=> D=1 i P=1
Wniosek:
Jaś zaprojektował sterownie windą w logice dodatniej (bo J)
II.
Pani przedszkolanka do Zuzi (lat 5):
Powiedz nam Zuziu kiedy winda nie jedzie (~J=1)?
Zuzia:
A2.
Winda nie jedzie (~J=1) wtedy i tylko wtedy gdy drzwi nie są zamknięte (~D=1) lub nie jest wciśnięty przycisk piętro (~P=1)
A2: ~J = ~D + ~P
co w logice jedynek oznacza:
~J=1 = ~D=1 lub ~P=1
Wniosek:
Zuzia zaprojektowała sterowanie windą w logice ujemnej (bo ~J)
Wnioski końcowe:
Rozwiązanie Jasia i Zuzi są matematycznie tożsame bo oczywisty związek logiki dodatniej (bo J) i ujemnej (bo ~J) jest następujący:
Jaś:
Moja logika dodatnia (bo J) to zanegowana logika ujemna (bo ~J), stąd mamy:
J = ~(~J)
Po podstawieniu:
A2: ~J = ~D + ~P
Mamy:
J = ~(~D+~P)
czyli:
J = ~(~D+~P) = D*P - prawo De Morgana
cnd
Zuzia:
Moja logika ujemna (bo ~J) to zanegowana logika dodatnia (bo J), stąd mamy:
~J = ~(J)
Po podstawieniu:
A1: J=D*P
Mamy:
~J = ~(D*P)
czyli:
~J = ~(D*P) = ~D+~P - prawo De Morgana
cnd
Doskonale tu widać, zarówno Jaś jak i Zuzia (oboje po 5 wiosenek) perfekcyjnie znają algebrę Kubusia bo po prostu pod nią podlegają.
Zachodzi matematyczna tożsamość:
Spójnik „i”(*) z języka potocznego = znana inżynierom bramka AND
Spójnik „lub”(+) z języka potocznego = znana inżynierom bramka OR
Znaczek przeczenia (~) też ma swój odpowiednik w bramkach logicznych w postaci układu negatora:
„o”(~) - bramka negatora „o”(~) w każdej chwili czasowej zamienia cyfrowy sygnał wejściowy (p) na jego negację na wyjściu negatora (~p).
Stąd:
Przełożenie powyższych zdań na bramki logiczne jest trywialne:
Wszędzie, gdzie wymawiamy spójnik „i”(*) walimy bramę AND.
Wszędzie, gdzie wymawiamy spójnik „lub”(+) walimy bramkę OR
Stąd:
Zdania Jasia i Zuzi w przełożeniu na teorię bramek logicznych wyglądają następująco:
| Kod: |
T1
Zdania Jasia i Zuzi przełożone na język bramek logicznych „i”(*) i „lub”(+)
-------------
D------x-------->| |
| | „i”(*) |---x-----x----> A1: J=D*P (Jaś)
P--x------------>| | | |
| | ------------- \/ |
| | o o # (negator w obu kierunkach)
| | ~D ------------- | /\
| |--o----->| | | |
| ~P | „lub”(+) |---x-----x----> A2: ~J=~D+~P (Zuzia)
|------o----->| |
-------------
Opis działania układu:
Jaś:
A1:
Winda jedzie (J) gdy drzwi są zamknięte (D) i wciśnięty przycisk piętro (P)
J=D*P
… a kiedy winda nie jedzie (~J)?
#
Dowolną funkcję logiczną (np. J=D*P) mamy prawo dwustronnie zanegować (#)
Negujemy funkcję logiczną A1 dwustronnie:
Zuzia:
A2:
~J=~(D*P)=~D+~P - prawo De Morgana
Stąd:
A2.
Winda nie jedzie (~J) gdy drzwi nie są zamknięte (~D)
lub nie jest wciśnięty przycisk piętro (~P)
~J=~D+~P
Gdzie:
# - dowolna strona znaczka # jest negacją drugiej strony
„o”(~) - bramka negatora „o”(~)
Negator w każdej chwili czasowej zamienia cyfrowy sygnał wejściowy
na jego negację na wyjściu negatora.
|
To jest cała filozofia przełożenia logiki matematycznej Jasia i Zuzi na teorię bramek logicznych.
Uwaga:
W użytecznym sterowaniu trzeba wprowadzić dodatkową zmienną binarną sygnalizującą dojechanie windy na żądane piętro, gdzie winda automatycznie staje. Przy zamkniętych drzwiach warunkiem koniecznym i wystarczającym kolejnej jazdy jest wciśnięcie piętra różnego od tego, na którym winda aktualnie stoi. Takie sterownie to temat na ćwiczenie laboratoryjne na I roku studiów elektronicznych.
Podsumowanie:
Matematyczna trudność projektowania złożonych sterowań w laboratorium bramek logicznych na I roku elektroniki Politechniki Warszawskiej absolutnie nie wykracza poza opisany wyżej poziom matematyczny 5-cio letnich, genialnych inżynierów Jasia i Zuzi. Oczywiście w trudniejszych problemach zmiennych binarnych jest więcej, ale układ sterowania projektuje się identycznie jak to zrobili Jaś i Zuzia, czyli mając w głębokim poważaniu jakiekolwiek tabele zero-jedynkowe.
Wyobraźmy sobie teraz mój szok 26 lat po studiach (rok 2006) kiedy pierwszy raz w życiu na forum śfinia usłyszałem takie pojęcie jak „Klasyczny Rachunek Zdań” oraz zobaczyłem przykładowe zdania prawdziwe w logice „matematycznej” ziemskich matematyków:
Jeśli 2+2=5 to 2+2=4
Jeśli 2+2=4 to Płock leży nad Wisłą
Jeśli Napoleon był kobietą to ja jestem jego ciotką
etc
Oczywistym jest, że się we mnie zagotowało a scyzoryk w kieszeni sam się otworzył bo jako zawodowy projektant sterowań w bramkach logicznych dla mnie naturalne zdania warunkowe „Jeśli p to q” wyglądały wyłącznie jak zdania Jasia i Zuzi wyżej, czyli była to 100% naturalna logika matematyczna człowieka, teraz wiem, że była to algebra Kubusia.
Wszyscy wiedzą, że czegoś nie da się zrobić, aż znajdzie się taki jeden, który nie wie, że się nie da, i on to robi.
Albert Einstein
Oczywiście 16 lat temu, gdy dzięki forum śfinia zaczynałem na serio moją przygodę z logiką matematyczną przez myśl mi nie przeszło, że z algebrą Boole’a może być cokolwiek nie w porządku, że jest ona wewnętrznie sprzeczna na poziomie funkcji logicznych algebry Boola’a.
Jedyną pewną metodą unikania porażek jest nie mieć żadnych, nowych pomysłów.
Albert Einstein
[link widoczny dla zalogowanych]
| Wikipedia napisał: |
Paradygmat (gr. παράδειγμα parádeigma „przykład, wzór”) – w rozumieniu wprowadzonym przez filozofa Thomasa Kuhna w książce Struktura rewolucji naukowych (The Structure of Scientific Revolutions) opublikowanej w 1962 roku – to zbiór pojęć i teorii tworzących podstawy danej nauki. Teorii i pojęć tworzących paradygmat raczej się nie kwestionuje, przynajmniej do czasu, kiedy paradygmat jest twórczy poznawczo – tzn. za jego pomocą można tworzyć teorie szczegółowe zgodne z danymi doświadczalnymi (historycznymi), którymi zajmuje się dana nauka.
Paradygmat w nauce
W 13 rozdziałach Kuhn dowodzi, że nauka nie jest jednostajnym, kumulatywnym pozyskiwaniem wiedzy. Zamiast tego nauka jest serią spokojnych okresów przerywanych przez gwałtowne intelektualne rewolucje, po których jeden koncepcyjny światopogląd jest zamieniany przez inny. Kuhn spopularyzował w tym kontekście termin paradygmat, opisywany przez niego jako w istocie zbiór poglądów podzielanych przez naukowców, zestaw porozumień o pojmowaniu zagadnień. Pomimo tego krytycy zarzucali mu brak precyzji w stosowaniu tego terminu.
Zgodnie z poglądami Kuhna paradygmat jest istotny dla badań naukowych, gdyż „żadna nauka przyrodnicza nie może być wyjaśniana bez zastosowania splecionych teoretycznych i metodologicznych poglądów pozwalających na wybór, ocenę i krytykę”.
Paradygmat kieruje wysiłkiem badawczym społeczności naukowych i jest tym kryterium, które najbardziej ściśle identyfikuje obszary nauk. Fundamentalnym argumentem Kuhna jest to, że dla dojrzałej nauki typową drogą rozwojową jest kolejne przechodzenie w procesie rewolucji od jednego do innego paradygmatu. Gdy ma miejsce zmiana paradygmatu, „świat naukowy zmienia się jakościowo i jest jakościowo wzbogacany przez fundamentalnie nowe zarówno fakty, jak i teorie”.
Kuhn utrzymywał także, że – wbrew obiegowym opiniom – typowi naukowcy nie są obiektywnymi i niezależnymi myślicielami, a są konserwatystami, którzy godzą się z tym, czego ich nauczono i stosują tę naukę (wiedzę) do rozwiązywania problemów zgodnie z dyktatem wyuczonej przez nich teorii. Większość z nich w istocie jedynie składa układanki, celując w odkrywaniu tego, co i tak już jest im znane - „Człowiek, który usiłuje rozwiązać problem zdefiniowany przez istniejącą wiedzę i technikę nie ma szerszych horyzontów. Wie on co chce osiągnąć, i w zgodzie z tym projektuje swoje narzędzia i kieruje swoimi myślami”.
Paradygmat a rewolucja naukowa
W czasach nauki instytucjonalnej (określenie również wprowadzone przez Kuhna) podstawowym zadaniem naukowców jest doprowadzenie uznanej teorii i faktów do najściślejszej zgodności.
W konsekwencji naukowcy mają tendencję do ignorowania odkryć badawczych, które mogą zagrażać istniejącemu paradygmatowi i spowodować rozwój nowego, konkurencyjnego paradygmatu.
Na przykład Ptolemeusz spopularyzował pogląd, że Słońce obiega Ziemię, i to przekonanie było bronione przez stulecia nawet w obliczu obalających go dowodów. Jak zaobserwował Kuhn, w trakcie rozwoju nauki „nowości wprowadzane są z trudem i z towarzyszącym mu, zgodnym z oczekiwaniami, jawnym oporem”. I tylko młodzi uczeni, nie tak głęboko indoktrynowani przez uznane teorie – jak Newton, Lavoisier lub Einstein – mogą dokonać odrzucenia starego paradygmatu.
Takie rewolucje naukowe następują tylko po długich okresach nauki instytucjonalnej, tradycyjnie ograniczonej ramami, w których musiała się ona (nauka) znajdować i zajmować się badaniami, zanim mogła te ramy zniszczyć”. Zresztą kryzys zawsze niejawnie tai się w badaniach, ponieważ każdy problem, który nauka instytucjonalna postrzega jako łamigłówkę, może być ujrzany z innej perspektywy, jako sprzeczność (wyłom), a zatem źródło kryzysu – jest to „istotne obciążenie” badań naukowych.
Kryzysy w nauce
Kryzysy są wyzwalane, gdy uczeni uznają odkryte sprzeczności za anomalię w dopasowaniu istniejącej teorii z naturą. Wszystkie kryzysy są rozwiązywane na trzy sposoby:
1.
Nauka instytucjonalna może udowodnić zdolność do objęcia kryzysowego problemu, i w tym przypadku wszystko wraca do „normalności”.
2.
Alternatywnie, problem pozostaje, jest zaetykietowany, natomiast postrzega się go jako wynik niemożności użycia niezbędnych przyrządów do rozwiązania go, więc uczeni pozostawiają go przyszłym pokoleniom z ich bardziej rozwiniętymi (zaawansowanymi) przyborami.
3.
W niewielu przypadkach pojawia się nowy kandydat na paradygmat, i wynika bitwa o jego uznanie będąca w istocie wojną paradygmatów.
Kuhn argumentuje, że rewolucje naukowe są nieskumulowanym epizodem rozwojowym, podczas którego starszy paradygmat jest zamieniany w całości lub po części przez niezgodny z nim paradygmat nowszy. Ale nowy paradygmat nie może być zbudowany na poprzedzającym go, a raczej może go tylko zamienić, gdyż „instytucjonalna tradycja naukowa wyłaniająca się z rewolucji naukowej jest nie tylko niezgodna, ale też nieuzgadnialna z tą, która pojawiła się przed nią”.
Rewolucja kończy się całkowitym zwycięstwem jednego z dwóch przeciwnych obozów.
|
W algebrze Kubusia zdecydowanie chodzi o punkt 3, bowiem w „Algebrze Kubusia” 100% definicji z zakresu logiki matematycznej jest sprzecznych z jakąkolwiek logiką matematyczną ziemskich matematyków np. „Klasycznym Rachunkiem Zdań”.
Dlaczego „Algebra Kubusia” będzie największym wydarzeniem w dziejach ludzkości?
Algebra Kubusia powstawała sukcesywnie w ciągu ostatnich 16 lat na bazie dyskusji, głównie na forum śfinia, to około 30 000 postów wyłącznie w temacie logiki matematycznej (średnio 5 postów dziennie non-stop).
Wszelkie nowinki wyklute w czasie tej dyskusji natychmiast nanosiłem do algebry Kubusia.
Wyszła z tego algebra Kubusia potwornie wielka z milionem różnych szczególików, nie nadająca się jako podręcznik logiki matematycznej do I klasy LO.
Od 17 grudnia 2021 roku piszę algebrę Kubusia zupełnie od nowa, gdzie skupiam się na najprostszym wyłożeniu fundamentów algebry Kubusia a nie mnożeniu przykładów z tysiącem mało istotnych szczególików.
W historii już coś takiego przerobiłem, dzięki czemu wiem jak z tego wybrnąć.
W 1983r, trzy lata po skończeniu elektroniki na Politechnice Warszawskiej zrobiłem fajny, mikroprocesorowy sterownik edukacyjny dla hobbystów (na i8085), który zacząłem sprzedawać na giełdzie elektronicznej w Warszawie.
Szybko okazało się, że moje dziecko jest bardzo słabo sprzedawalne z prostej przyczyny - wiedza ówczesnych hobbystów elektroniki w obszarze mikroprocesorów była praktycznie zerowa.
Wpadłem wówczas na pomysł napisania serii podręczników do elektroniki przy założeniu, że odbiorca nie zna prawa Ohma, czyli z założenie były to podręczniki dla I klasy LO, gdzie po łagodnej równi pochyłej czytelnik był prowadzony od takich pojęć jak napięcie, prąd, prawo Ohma … poprzez elektronikę klasyczną, układy scalone średniej skali integracji, układy mikroprocesorowe, do praktycznego programowania różnych sterowań w j. asemblera Z80 przy pomocy opracowanego przeze mnie sterownika.
Po dwóch latach pracy dzieło ukończyłem z sukcesem, mój sterownik do dziś jest legendą wśród starszej daty elektroników.
Przykładowa dwie recenzje to:
1.
Serdecznie dziękuję za dwa pierwsze podręczniki do nauki elektroniki i mikroelektroniki. Są one naprawdę doskonale napisane. Mimo, że przesyłkę otrzymałem dwa dni temu to już zdążyłem je obie przeczytać - bardzo trudno się od nich oderwać.
Obecnie jestem uczniem I klasy Technikum Elektronicznego …
2.
Jestem zachwycony Pańskimi książkami na temat mikroprocesorów. Książki są wyjątkowo przejrzyście napisane. Takiej metodyki mogą pozazdrościć najlepsze uczelnie w kraju, jednej z nich jestem absolwentem.
Już choćby z powyższego widać, że dokumentacja opracowanego przeze mnie sterownika mikroprocesorowego była pasjonującą lekturą zarówno dla 15 latka, jak i absolwenta wyższej uczelni.
Geneza mojego sukcesu sprzed 37 lat:
Tematem mojej pracy magisterskiej było praktyczne wykonanie systemu dwuprocesorowego (na i8080) ze wspólną pamięcią i wspólną szyną danych (rok 1980!), gdzie na odbiorze zademonstrowałem, iż system ten przetwarza dane z dwukrotnie większą szybkością niż system jednoprocesorowy … po czym bez żadnych pytań dodatkowych dostałem w indeksie 5.
Na studiach elektronicznych wykładana jest bardzo rozległa wiedza szczegółowa z różnych dziedzin elektroniki której nie sposób spamiętać i wykorzystać w przyszłości. Oczywistym jest, że absolwent elektroniki wybiera wąską specjalizację i rozwija się wyłącznie w tej dziedzinie co oznacza, że wiedza mu niepotrzebna jest zapominana mimo że musiał ją zaliczyć na studiach.
Ja wybrałem (już na studiach) specjalizację w zakresie wszelkich sterowań w technice mikroprocesorowej i tylko tą wiedzę przekazałem w moich podręcznikach do nauki elektroniki dla hobbystów.
Fundament mojego sukcesu był następujący:
W trakcie pisania podręczników miałam zakaz zaglądania do jakichkolwiek podręczników akademickich i innej literatury elektronicznej (dotrzymany w 100%) celem przypomnienia sobie tego i owego wychodząc z założenia, iż skoro czegoś tam nie pamiętam to nie jest to potrzebne w praktyce sterowań i programowania mikroprocesorów.
To co zrobiłem 37 lat temu, było fajne, ale w gruncie rzeczy przekazałem znaną wiedzę praktyczną o elektronice w najprostszy możliwy sposób.
Algebra Kubusia to jednak fundamentalnie co innego!
Pisząc od 16 lat algebrę Kubusia ja nie przekazuję aktualnej wiedzy matematycznej z zakresu logiki matematycznej w prostszy sposób jak to zrobiłem z elektroniką 37 lat temu.
Ja, aktualną wiedzę matematyczną z zakresu logiki matematycznej totalnie neguję bowiem w algebrze Kubusia 100% definicji z zakresu logiki matematycznej jest sprzecznych z jakąkolwiek logiką matematyczną znaną ziemskim matematykom.
Założenie mam identyczne jak 37 lat temu:
Po prostu muszę założyć, że wiedza aktualnych ziemskich matematyków w zakresie jedynej poprawnej logiki matematycznej, jaką jest algebra Kubusia, której naturalnymi ekspertami są 5-cio latki … jest równa zeru absolutnemu!
Mam nadzieję, że osiągnę sukces i koniec końców ziemscy matematycy zaakceptują algebrę Kubusia jako jedyną poprawną logikę matematyczną obowiązującą w naszym Wszechświecie.
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Nie 21:28, 27 Mar 2022 Temat postu: Wysłany: Nie 21:28, 27 Mar 2022 Temat postu: |
|
|
Nowy wstęp do algebry Kubusia!
Ze starego wstępu (post wyżej) zostało kilka zdań.
W nowym wstępie prezentuję w skrócie definicje wszystkich znaczków używanych w algebrze Kubusia, bowiem wszystkie są sprzeczne z jakakolwiek logiką matematyczną ziemskich matematyków - mają inne definicje.
Algebra Kubusia - matematyka języka potocznego
W trakcie pisania
2022-03-09
Powstaje najnowsza wersja algebry Kubusia, zminimalizowana do najważniejszych definicji i praw algebry Kubusia.
Autor:
Kubuś ze 100-milowego lasu
Rozszyfrowali:
Rafal3006 i przyjaciele
Dziękuję wszystkim, którzy dyskutując z Rafałem3006 przyczynili się do odkrycia algebry Kubusia (cytuję w kolejności zaistnienia):
Wuj Zbój, Miki (vel Lucek), Volrath, Macjan, Irbisol, Makaron czterojajeczny, Quebab, Windziarz, Fizyk, Idiota, Sogors (vel Dagger), Fiklit, Yorgin, Pan Barycki, Zbigniewmiller, Mar3x, Wookie, Prosiak, Andy72, Michał Dyszyński, Szaryobywatel, Jan Lewandowski, MaluśnaOwieczka i inni.
Kluczowi przyjaciele Kubusia, dzięki którym algebra Kubusia została rozszyfrowana to (cytuję w kolejności zaistnienia):
1.
Rafał3006
2.
Wuj Zbój - dzięki któremu Rafal3006 poznał istotę implikacji od strony czysto matematycznej.
3.
Fiklit - który poświęcił 8 lat życia na cierpliwe tłumaczenie Rafałowi3006 jak wygląda otaczający nas świat z punktu widzenia Klasycznego Rachunku Zdań
Bez Fiklita o rozszyfrowaniu algebry Kubusia moglibyśmy wyłącznie pomarzyć
4.
Irbisol - znakomity tester końcowej wersji algebry Kubusia, za wszelką cenę usiłujący ją obalić.
Czyż można sobie wymarzyć lepszego testera?
5.
MaluśnaOwieczka - końcowy uczestnik dyskusji o algebrze Kubusia w trakcie której wiele definicji zostało doprecyzowanych.
Niniejszy podręcznik jest końcowym efektem 16-letniej dyskusji na forach śfinia, ateista.pl i yrizona - to około 30 000 postów, średnio 5 postów dziennie wyłącznie na temat logiki matematycznej.

Spis treści:
1.0 Operatory jednoargumentowe
2.0 Podstawowa algebra Boole’a
2.7 Geneza błędu czysto matematycznego prof. L. Newelskiego
3.0 Dwuargumentowe funkcje logiczne
4.0 Operatory Y|=f(x) z grupy TF0-TF3 wyrażone spójnikami „i”(*) i „lub”(+)
5.0 Kubusiowa teoria zbiorów
6.0 Fundamenty obsługi zdań warunkowych w algebrze Kubusia
7.0 Spójniki obsługujące zdania warunkowe „Jeśli p to q”
8.0 Implikacja prosta p|=>q i odwrotna p|~>q
8.1 Implikacja prosta p|=>q w logice dodatniej (bo q)
8.4 Implikacja odwrotna p|~>q w logice dodatniej (bo q)
8.7 Implikacja prosta p|=>q vs implikacja odwrotna p|~>q
8.9 Geneza tabel zero-jedynkowych warunku wystarczającego => i koniecznego ~>
9.0 Spójniki równoważności p<=>q i „albo”($) p$q
9.1 Równoważność p<=>q w zbiorach
9.4 Równoważność p<=>q w zdarzeniach
9.5 Przykłady równoważności w zbiorach TP<=>SK i zdarzeniach A<=>S
Wstęp:
Ja, Rafal3006, przez ostatnie 16 lat wraz z przyjaciółmi (uczestnikami dyskusji) intensywnie pracowałem (około 30 000 postów) nad rozszyfrowaniem algebry Kubusia, której rzeczywistym autorem jest Kubuś, stwórca naszego Wszechświata.
Formalnie algebry Kubusia nie musimy się uczyć bo po prostu pod nią polegamy nie mając żadnych szans, aby się od niej uwolnić. Wynika z tego, że ekspertem algebry Kubusia jest każdy człowiek (od 5-cio latka poczynając) tylko póki co, o tym nie wie. Algebra Kubusia to również podłożenie matematyki pod język potoczny człowieka, czyli coś, o czym matematycy marzą od 2500 lat (od Sokratesa).
Po co komu algebra Kubusia skoro wszyscy jesteśmy jej ekspertami?
Pytanie analogiczne to:
Po co komu znajomość gramatyki języka polskiego, skoro 5-cio latek biegle posługuje się językiem ojczystym nie znając formalnej gramatyki języka?
Osobiście nigdy nie znałem i nie znam formalnej gramatyki języka polskiego tzn. nie wiem co to jest jakiś tam podmiot, orzeczenie, przysłówek etc. … a po polsku potrafię pisać.
Mam nadzieję, że koniec końców ziemscy matematycy zaakceptują algebrę Kubusia jako jedyną poprawną logikę matematyczną obowiązującą w naszym Wszechświecie.
Notacja (N) w algebrze Kubusia:
100% znaczków używanych w algebrze Kubusia ma inne definicje niż w jakiejkolwiek logice matematycznej ziemskich matematyków. Konieczne jest zatem podanie skrótowych definicji (wraz z przykładami) wszystkich znaczków używanych w algebrze Kubusia, co niniejszym czynimy.
Spis treści
N1 Znaczki algebry Boole’a 4
N2 Fundamentalne znaczki obsługujące zdania warunkowe „Jeśli p to q” 4
N2.1 Definicja elementu wspólnego zbiorów ~~> 5
N2.2 Definicja warunku wystarczającego => w zbiorach 5
N2.3 Definicja warunku koniecznego ~> w zbiorach 6
N2.4 Definicja kontrprzykładu w zbiorach 7
N2.5 Prawa Prosiaczka 7
N3 Fundament algebry Kubusia w obsłudze zdań warunkowych „Jeśli p to q” 9
N3.1 Prawo Sowy 9
N3.2 Definicja dowodu „nie wprost” w algebrze Kubusia 9
N4 Fundamentalne tożsamości pojęć w algebrze Kubusia 9
N5 Prawo Słonia dla zbiorów 10
N6 Prawo Irbisa 12
N6.1 Prawo Irbisa dla zbiorów 12
N6.2 Prawo Irbisa dla zdarzeń 15
N7 Pozostałe znaczki w algebrze Kubusia 16
N7.1 Implikacja prosta p|=>q 16
N7.2 Implikacja odwrotna p|~>q 17
N7.3 Równoważność p<=>q 18
N7.4 Spójnik „albo”($) 18
N7.5 Chaos p|~~>q 18
N1 Znaczki algebry Boole’a
Algebra Boole’a to zaledwie 5 znaczków:
1 - prawda
0 - fałsz
(~) - negacja
„i”(*) - spójnik „i”(*) z języka potocznego
„lub”(+) - spójnik „lub”(+) z języka potocznego
N2 Fundamentalne znaczki obsługujące zdania warunkowe „Jeśli p to q”
Fundament obsługi zdań warunkowych „Jeśli p to q” to zaledwie trzy znaczki:
1.
Element wspólny zbiorów p~~>q lub zdarzenie możliwe p~~>q:
Jeśli p to q
Zbiory:
p~~>q =p*q=1 - istnieje (=1) element wspólny zbiorów p i q
Zdarzenia:
p~~>q =p*q=1 - możliwe jest (=1) jednoczesne zajście zdarzeń p i q
Inaczej:
p~~>q=p*q=0
2.
Warunek wystarczający p=>q:
Jeśli p to q”
p=>q =1 - zajście p jest wystarczające => dla zajścia q
Inaczej:
p=>q=0
3.
Warunek konieczny p~>q:
Jeśli p to q
p~>q =1 - zajście p jest konieczne ~> dla zajścia q
inaczej:
p~>q=0
N2.1 Definicja elementu wspólnego zbiorów ~~>
Definicja elementu wspólnego ~~> zbiorów:
Jeśli p to q
p~~>q =p*q =1
Definicja elementu wspólnego zbiorów ~~> jest spełniona (=1) wtedy i tylko wtedy gdy zbiory p i q mają co najmniej jeden element wspólny
Inaczej:
p~~>q= p*q= [] =0 - zbiory p i q są rozłączne, nie mają (=0) elementu wspólnego ~~>
Decydujący w powyższej definicji jest znaczek elementu wspólnego zbiorów ~~>, dlatego dopuszczalny jest zapis skrócony p~~>q.
W operacji iloczynu logicznego zbiorów p*q poszukujemy jednego wspólnego elementu, nie wyznaczamy kompletnego zbioru p*q.
Jeśli zbiory p i q mają element wspólny ~~> to z reguły błyskawicznie go znajdujemy:
p~~>q=p*q =1
co na mocy definicji kontrprzykładu (poznamy za chwilkę) wymusza fałszywość warunku wystarczającego =>:
p=>~q =0 (i odwrotnie)
Przykład:
Jeśli dowolna liczba jest podzielna przez 8 to może ~~> być podzielna przez 3
P8~~>P3 = P8*P3 =1
Istnieje (=1) wspólny element zbiorów P8=[8,16,24..] i P3=[3,6,9..24..] np. 24
N2.2 Definicja warunku wystarczającego => w zbiorach
Wstęp:
Definicja podzbioru => w algebrze Kubusia:
Zbiór p jest podzbiorem => zbioru q wtedy i tylko wtedy gdy wszystkie elementy zbioru p należą do zbioru q
p=>q =1 - wtedy i tylko wtedy gdy relacja podzbioru => jest (=1) spełniona
Inaczej:
p=>q =0 - wtedy i tylko wtedy gdy relacja podzbioru => nie jest (=0) spełniona
Finał:
Definicja warunku wystarczającego => w zbiorach:
Jeśli p to q
p=>q =1
Zajście p jest (=1) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => jest (=1) spełniona wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Inaczej:
p=>q =0
Zajście p nie jest (=0) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => nie jest (=0) spełniona wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Matematycznie zachodzi tożsamość:
Warunek wystarczający => = relacja podzbioru => = twierdzenie proste „Jeśli p to q” =>
Definicja warunku wystarczającego => dla potrzeb rachunku zero-jedynkowego:
p=>q = ~p+q
Przykład twierdzenia matematycznego:
A1.
Jeśli dowolna liczba jest podzielna przez 8 to na 100% => jest podzielna przez 2
Innymi słowy:
Każda liczba podzielna przez 8 jest podzielna przez 2
P8=>P2 =1
Podzielność dowolnej liczby przez 8 jest warunkiem wystarczającym => dla jej podzielności przez 2 bo zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8..]
Definicja warunku wystarczającego => jest spełniona (=1) bo zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8..]
cnd
(dowód przez pokazanie)
N2.3 Definicja warunku koniecznego ~> w zbiorach
Wstęp:
Definicja nadzbioru ~> w algebrze Kubusia:
Zbiór p jest nadzbiorem ~> zbioru q wtedy i tylko wtedy gdy zbiór p zawiera co najmniej wszystkie elementy zbioru q
p~>q =1 - wtedy i tylko wtedy gdy relacja nadzbioru ~> jest (=1) spełniona
Inaczej:
p~>q =0 - wtedy i tylko wtedy gdy relacja nadzbioru ~> nie jest (=0) spełniona
Finał:
Definicja warunku koniecznego ~> w zbiorach:
Jeśli p to q
p~>q =1
Zajście p jest (=1) konieczne ~> dla zajścia q wtedy i tylko wtedy gdy zbiór p jest (=1) nadzbiorem ~> zbioru q
Innymi słowy:
Definicja warunku koniecznego ~> jest (=1) spełniona wtedy i tylko wtedy gdy zbiór p jest (=1) nadzbiorem ~> zbioru q
Inaczej:
p~>q =0
Zajście p nie jest (=0) konieczne ~> dla zajścia q wtedy i tylko wtedy gdy zbiór p nie jest (=0) nadzbiorem ~> zbioru q
Innymi słowy:
Definicja warunku koniecznego ~> nie jest (=0) spełniona wtedy i tylko wtedy gdy zbiór p nie jest (=0) nadzbiorem ~> zbioru q
Matematycznie zachodzi tożsamość:
Warunek konieczny ~> = relacja nadzbioru ~>
Definicja warunku koniecznego ~> dla potrzeb rachunku zero-jedynkowego:
p~>q = p+~q
Przykład:
B1.
Jeśli dowolna liczba jest podzielna przez 2 to może ~> być podzielna przez 8
P2~>P8 =1
Podzielność dowolnej liczby przez 2 jest warunkiem koniecznym ~> dla jej podzielności przez 8 bo zbiór P2=[2,4,6,8..] jest nadzbiorem ~> zbioru P8=[8,16,24..]
Innymi słowy:
Definicja warunku koniecznego ~> jest spełniona (=1) bo zbiór P2=[2,4,6,8..] jest (=1) nadzbiorem ~> zbioru P8=[8,16,24..]
cnd
(dowód przez pokazanie)
N2.4 Definicja kontrprzykładu w zbiorach
Definicja kontrprzykładu w zbiorach:
Kontrprzykładem dla warunku wystarczającego p=>q nazywamy to samo zdanie z zanegowanym następnikiem kodowane elementem wspólnym zbiorów p~~>~q=p*~q
Rozstrzygnięcia:
Prawdziwość warunku wystarczającego p=>q=1 wmusza fałszywość kontrprzykładu p~~>~q=p*~q=0 (i odwrotnie)
Fałszywość warunku wystarczającego p=>q=0 wmusza prawdziwość kontrprzykładu p~~>~q=p*~q=1 (i odwrotnie)
Przykład:
A1.
Jeśli dowolna liczba jest podzielna przez 8 (P8) to na 100% => jest podzielna przez 2 (P2)
P8=>P2=1
Podzielność dowolnej liczby przez 8 jest warunkiem wystarczającym => dla jej podzielności przez 2, bo zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8…], co każdy matematyk bez trudu udowodni.
cnd
Na mocy definicji kontrprzykładu, z prawdziwości warunku wystarczającego A1 wynika fałszywość kontrprzykładu A1’ (i odwrotnie)
A1’
Jeśli dowolna liczba jest podzielna przez 8 (P8) to może ~~> nie być podzielna przez 2 (~P2)
P8~~>~P2 = P8*~P2 =[] =0
Nie istnieje (=0) wspólny element zbiorów P8=[8,16,24..] i ~P2=1,3,5,7,9…] bo zbiory te są rozłączne.
Na mocy definicji kontrprzykładu nie musimy udowadniać w sposób bezpośredni iż zbiór P8=[8,16,24..] jest rozłączny ze zbiorem liczb nieparzystych ~P2=[1,3,5,7,9..], bowiem dowód „nie wprost” tego faktu wynika z definicji kontrprzykładu.
Uwaga na standard w algebrze Kubusia:
Kontrprzykład dla warunku wystarczającego => A1 oznaczamy A1’
N2.5 Prawa Prosiaczka
Kontynuujmy rozważania na temat powyższego przykładu.
A1.
Jeśli dowolna liczba jest podzielna przez 8 (P8) to na 100% => jest podzielna przez 2 (P2)
P8=>P2=1
Podzielność dowolnej liczby przez 8 jest warunkiem wystarczającym => dla jej podzielności przez 2, bo zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8…], co każdy matematyk bez trudu udowodni.
cnd
Na mocy definicji kontrprzykładu, z prawdziwości warunku wystarczającego A1 wynika fałszywość kontrprzykładu A1’ (i odwrotnie)
A1’
Jeśli dowolna liczba jest podzielna przez 8 (P8) to może ~~> nie być podzielna przez 2 (~P2)
P8~~>~P2 = P8*~P2 =[] =0
Nie istnieje (=0) wspólny element zbiorów P8=[8,16,24..] i ~P2=1,3,5,7,9…] bo zbiory te są rozłączne.
Na mocy definicji kontrprzykładu nie musimy udowadniać w sposób bezpośredni iż zbiór P8=[8,16,24..] jest rozłączny ze zbiorem liczb nieparzystych ~P2=[1,3,5,7,9..], bowiem dowód „nie wprost” tego faktu wynika z definicji kontrprzykładu.
Prawa Prosiaczka:
(p=1)=(~p=0)
(~p=1)=(p=0)
I prawo Prosiaczka:
Prawda (=1) w logice dodatniej (bo p) jest tożsama z fałszem (=0) w logice ujemnej (bo ~p)
(p=1)=(~p=0)
##
II prawo Prosiaczka:
Prawda (=1) w logice ujemnej (bo ~p) jest tożsama z fałszem (=0) w logice dodatniej (bo p)
(~p=1)=(p=0)
Gdzie:
## - różne na mocy definicji
Prawa Prosiaczka w praktyce na przykładzie wyżej:
A1’: P8~~>~P2=P8*~P2=1*1=0
Powyższa linia rozpisana szczegółowo przyjmuje postać:
A1’: Yb = P8~~>~P2=P8*~P2=1*1=0
Zapis tożsamy to:
(Yb=0) <=> P8=1 i ~P2=1
Czytamy:
Fałszem jest (=0) że istnieje wspólny element ~~> (Yb) zbiorów P8=[8,16,24..] i ~P2=[1,3,5,7,9..]
Prawo Prosiaczka:
(Yb=0)=(~Yb=1)
Stąd tożsamy zapis szczegółowy:
A1’: ~Yb=P8~~>~P2=P8*~P2=1*1=1
Zapis tożsamy to:
(~Yb=1) <=> P8=1 i ~P2=1
Czytamy:
Prawdą jest (=1) że nie istnieje wspólny element ~~> (~Yb) zbiorów P8=[8,1624..] i ~P2=[1,3,5,7,9..]
Znaczenie symboli:
Yb - istnieje wspólny element ~~>
~Yb - nie istnieje wspólny element ~~>
N3 Fundament algebry Kubusia w obsłudze zdań warunkowych „Jeśli p to q”
Matematyczne związki warunku wystarczającego => i koniecznego ~>.
| Kod: |
T0
Fundament algebry Kubusia w obsłudze zdań warunkowych „Jeśli p to q”
Matematyczne związki warunku wystarczającego => i koniecznego ~>:
A1B1: A2B2: | A3B3: A4B4:
A: 1: p=>q = 2:~p~>~q [=] 3: q~>p = 4:~q=>~p [=] 5: ~p+q
## ## ## ## ##
B: 1: p~>q = 2:~p=>~q [=] 3: q=>p = 4:~q~>~p [=] 5: p+~q
Prawa Kubusia: | Prawa kontrapozycji dla warunku wystarczającego =>:
A1: p=>q = A2:~p~>~q | A1: p=>q = A4:~q=>~p
B1: p~>q = B2:~p=>~q | B2:~p=>~q = B3: q=>p
Prawa Tygryska: | Prawa kontrapozycji dla warunku koniecznego ~>:
A1: p=>q = A3: q~>p | A2:~p~>~q = A3: q~>p
B1: p~>q = B3: q=>p | B1: p~>q = B4:~q~>~p
Gdzie:
## - różne na mocy definicji warunku wystarczającego => i koniecznego ~>
p i q muszą być wszędzie tymi samymi p i q inaczej błąd podstawienia
|
N3.1 Prawo Sowy
I Prawo Sowy
Dla udowodnienia prawdziwości wszystkich zdań serii Ax potrzeba i wystarcza udowodnić prawdziwość dowolnego zdania serii Ax
Dla udowodnienia fałszywości wszystkich zdań serii Ax potrzeba i wystarcza udowodnić fałszywość dowolnego zdania serii Ax
##
II Prawo Sowy
Dla udowodnienia prawdziwości wszystkich zdań serii Bx potrzeba i wystarcza udowodnić prawdziwość dowolnego zdania serii Bx
Dla udowodnienia fałszywości wszystkich zdań serii Bx potrzeba i wystarcza udowodnić fałszywość dowolnego zdania serii Bx
Gdzie:
## - różne na mocy definicji
N3.2 Definicja dowodu „nie wprost” w algebrze Kubusia
Definicja dowodu „nie wprost” w algebrze Kubusia:
Dowód „nie wprost” w algebrze Kubusia to dowód warunku koniecznego ~> lub wystarczającego => (twierdzenie proste „Jeśli p to q”) z wykorzystaniem praw logiki matematycznej (prawa Kubusia, prawa Tygryska, prawa kontrapozycji dla warunku wystarczającego =>, prawa kontrapozycji dla warunku koniecznego) plus definicja kontrprzykładu.
N4 Fundamentalne tożsamości pojęć w algebrze Kubusia
W algebrze Kubusia w zbiorach zachodzi tożsamość pojęć:
Warunek wystarczający A1: p=>q = relacja podzbioru A1: p=>q = twierdzenie proste p=>q=~p+q
##
Warunek konieczny B1: p~>q = relacja nadzbioru B1: p~>q = twierdzenie odwrotne B3: q=>p=~q+p
bo prawo Tygryska:
B1: p~>q = B3: q=>p = p+~q
Gdzie:
## - różne na mocy definicji
p i q musi być wszędzie tymi samymi p i q, inaczej błąd podstawienia
W algebrze Kubusia w zdarzeniach zachodzi tożsamość pojęć:
Warunek wystarczający A1: p=>q = twierdzenie proste A1: p=>q=~p+q
##
Warunek konieczny B1: p~>q = twierdzenie odwrotne B3: q=>p=~q+p
bo prawo Tygryska:
B1: p~>q = B3: q=>p = p+~q
Gdzie:
## - różne na mocy definicji
p i q musi być wszędzie tymi samymi p i q, inaczej błąd podstawienia
N5 Prawo Słonia dla zbiorów
Potrzebne definicje podstawowe:
1.
Definicja podzbioru =>:
Zbiór p jest podzbiorem => zbioru q wtedy i tylko wtedy gdy wszystkie elementy zbioru p należą do zbioru q
p=>q =1 - wtedy i tylko wtedy gdy relacja podzbioru => jest (=1) spełniona
Inaczej:
p=>q =0 - wtedy i tylko wtedy gdy relacja podzbioru => nie jest (=0) spełniona
2.
Definicja warunku wystarczającego => w zbiorach:
Jeśli p to q
p=>q =1
Zajście p jest (=1) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => jest (=1) spełniona wtedy i tylko wtedy gdy zbiór p jest (=1) podzbiorem => zbioru q
Inaczej:
p=>q =0
Zajście p nie jest (=0) wystarczające => dla zajścia q wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Innymi słowy:
Definicja warunku wystarczającego => nie jest (=0) spełniona wtedy i tylko wtedy gdy zbiór p nie jest (=0) podzbiorem => zbioru q
Prawo Słonia:
Matematycznie zachodzi tożsamość logiczna „=” dla zbiorów:
1: Warunek wystarczający => = 2: relacja podzbioru => = 3: twierdzenie „Jeśli p to q” =>
Gdzie:
„=” - znaczek tożsamości logicznej
Definicja tożsamości logicznej „=”:
Prawdziwość dowolnego członu z tożsamości logicznej „=” wymusza prawdziwość pozostałych członów.
Fałszywość dowolnego członu z tożsamości logicznej „=” wymusza fałszywość pozostałych członów.
Z definicji tożsamości logicznej wynika, że zapis tożsamy powyższej tożsamości pojęć jest następujący
Prawo Słonia:
Matematycznie zachodzi tożsamość logiczna <=> dla zbiorów:
1: Warunek wystarczający => <=> 2: relacja podzbioru => <=> 3: twierdzenie „Jeśli p to q” =>
Gdzie:
<=> - znaczek równoważności „wtedy i tylko wtedy”
„=”, <=> - tożsame znaczki tożsamości logicznej
Z definicji tożsamości logicznej <=> wynika, że:
a)
Udowodnienie prawdziwości dowolnego członu powyższej tożsamości logicznej (1 albo 2 albo 3) gwarantuje prawdziwość dwóch pozostałych członów
b)
Udowodnienie fałszywości dowolnego członu powyższej tożsamości logicznej (1 albo 2 albo 3) gwarantuje fałszywość dwóch pozostałych członów
Na mocy prawa Słonia i jego powyższej interpretacji, możemy dowodzić prawdziwość dowolnych zdań warunkowych "Jeśli p to q" mówiących o zbiorach metodą "nie wprost"
Przykładowe zadanie matematyczne w I klasie LO.
Zbadaj czy zachodzi warunek wystarczający => w poniższym zdaniu:
A1.
Jeśli dowolna liczba jest podzielna przez 8 to jest podzielna przez 2
P8=>P2=?
W metodzie "nie wprost" na mocy prawa Słonia dowodzimy prawdziwości relacji podzbioru =>
Innymi słowy badamy:
Czy zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8..]?
Oczywiście relacja podzbioru => jest (=1) tu spełniona:
P8=>P2=1
co każdy matematyk bez trudu udowodni.
W tym momencie na mocy prawa Słonia mamy udowodnione metodą "nie wprost" dwa fakty czysto matematyczne:
1.
Zdanie A1 jest prawdziwe
A1: P8=>P2 =1
2.
Podzielność dowolnej liczby przez 8 jest warunkiem wystarczającym => dla jej podzielności przez 2
A1: P8=>P2 =1
Podsumowując:
Z gołych definicji podzbioru => i warunku wystarczającego => nic w matematyce nie wynika, dopóki nie poznamy prawa Słonia.
Dopiero prawo Słonia w dowodzeniu prawdziwości warunku wystarczającego =>, czy też prawdziwości samego zdania warunkowego "Jeśli p to q" ma fundamentalne znaczenie, co udowodniono ciut wyżej.
Zauważmy, że identycznie mamy w świecie fizyki.
Przykład:
Możemy podać definicję prądu, możemy podać oddzielną definicję napięcia, oddzielną definicję rezystora … i nic z tego wynika dopóki nie poznamy prawa Ohma wiążącego te pojęcia.
N6 Prawo Irbisa
Prawo Irbisa:
Dowolna równoważność prawdziwa p<=>q=1 definiuje tożsamość zbiorów/zdarzeń p=q i odwrotnie
N6.1 Prawo Irbisa dla zbiorów
Prawo Irbisa dla zbiorów:
Dowolna równoważność prawdziwa p<=>q=1 definiuje tożsamość zbiorów p=q i odwrotnie
| Kod: |
T0
Fundament algebry Kubusia w obsłudze zdań warunkowych „Jeśli p to q”
Matematyczne związki warunku wystarczającego => i koniecznego ~>:
A1B1: A2B2: | A3B3: A4B4:
A: 1: p=>q = 2:~p~>~q [=] 3: q~>p = 4:~q=>~p [=] 5: ~p+q
## ## ## ## ##
B: 1: p~>q = 2:~p=>~q [=] 3: q=>p = 4:~q~>~p [=] 5: p+~q
Prawa Kubusia: | Prawa kontrapozycji dla warunku wystarczającego =>:
A1: p=>q = A2:~p~>~q | A1: p=>q = A4:~q=>~p
B1: p~>q = B2:~p=>~q | B2:~p=>~q = B3: q=>p
Prawa Tygryska: | Prawa kontrapozycji dla warunku koniecznego ~>:
A1: p=>q = A3: q~>p | A2:~p~>~q = A3: q~>p
B1: p~>q = B3: q=>p | B1: p~>q = B4:~q~>~p
Gdzie:
## - różne na mocy definicji warunku wystarczającego => i koniecznego ~>
p i q muszą być wszędzie tymi samymi p i q inaczej błąd podstawienia
|
A1B1:
Definicja równoważności p<=>q w logice dodatniej (bo q):
Równoważność p<=>q w logice dodatniej (bo q) to spełnienie zarówno warunku wystarczającego =>, jak i koniecznego ~> między tymi samymi punktami i w tym samym kierunku
A1: p=>q =1 - zajście p jest (=1) wystarczające => dla zajścia q
B1: p~>q =1 - zajście p jest (=1) konieczne ~> dla zajścia q
Stąd mamy definicję równoważności p<=>q w równaniu logicznym:
A1B1: p<=>q = (A1: p=>q)*(B1: p~>q) =1*1 =1
Czytamy:
Równoważność p<=>q w logice dodatniej (bo q) jest prawdziwa (=1) wtedy i tylko wtedy gdy
zajście p jest (=1) konieczne ~> (B1) i wystarczające => (A1) dla zajścia q
Powyższa definicja równoważności znana jest wszystkim ludziom (nie tylko matematykom):
Dowód:
Klikamy na googlach:
„konieczne i wystarczające”
Wyników: 8 630
„potrzeba i wystarcza”
Wyników: 49 000
Stąd mamy:
| Kod: |
TR
Tabela prawdy równoważności p<=>q
Matematyczne związki warunku wystarczającego => i koniecznego ~>
w równoważności p<=>q
A1: p=>q =1 - zajście p jest (=1) wystarczające => dla zajścia q
B1: p~>q =1 - zajście p jest (=1) konieczne ~> dla zajścia q
Stąd mamy definicję równoważności p<=>q w równaniu logicznym:
A1B1: p<=>q = (A1: p=>q)*(B1: p~>q) =1*1 =1
A1B1: A2B2: | A3B3: A4B4:
A: 1: p=>q = 2:~p~>~q [=] 3: q~>p = 4:~q=>~p [=] 5: ~p+q =1
## ## ## ## ##
B: 1: p~>q = 2:~p=>~q [=] 3: q=>p = 4:~q~>~p [=] 5: p+~q =1
Gdzie:
## - różne na mocy definicji warunku wystarczającego => i koniecznego ~>
p i q muszą być wszędzie tymi samymi p i q inaczej błąd podstawienia
|
Prawa Sowy dla równoważności p<=>q:
Prawdziwość dowolnego zdania serii Ax wymusza prawdziwość wszystkich zdań serii Ax
Prawdziwość dowolnego zdania serii Bx wymusza prawdziwość wszystkich zdań serii Bx
Jak dowodzi się prawdziwość równoważności w zbiorach p<=>q w matematyce klasycznej?
Na mocy prawa Sowy wszystko jest jasne i trywialne.
Matematyczna definicja równoważności p<=>q:
Równoważność p<=>q to jednoczesna prawdziwość twierdzenia prostego (A1: p=>q=1) i twierdzenia odwrotnego (B3: q=>p=1)
A1B3: p<=>q = (A1: p=>q)*(B3: q=>p) =1*1=1
Czytamy:
Równoważność w zbiorach p<=>q jest prawdziwa wtedy i tylko wtedy gdy prawdziwe jest twierdzenie proste A1: p=>q=1 i jednocześnie prawdziwe jest twierdzenie odwrotne B3: q=>p=1
Prawo Słonia:
W algebrze Kubusia w zbiorach zachodzi tożsamość pojęć:
Warunek wystarczający A1: p=>q = relacja podzbioru A1: p=>q = twierdzenie proste p=>q=~p+q
Stąd mamy:
Definicja równoważności w zbiorach:
Równoważność w zbiorach p<=>q jest prawdziwa wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q (A1: p=>q=1) i jednocześnie zbiór q jest podzbiorem => zbioru p (B3: q=>p=1)
A1B3: p<=>q = (A1: p=>q)*(B3: q=>p) =1*1=1
Czytamy:
Równoważność p<=>q jest prawdziwa (=1) wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q (A1: p=>q=1) i jednocześnie zbiór q jest podzbiorem => zbioru p (B3: q=>p=1)
Innymi słowy:
Równoważność p<=>q jest prawdziwa (=1) wtedy i tylko wtedy gdy spełniona jest relacja podzbioru => w dwie strony.
Zauważmy, że prawa strona to znana absolutnie każdemu matematykowi definicja tożsamości zbiorów p=q.
Definicja tożsamości zbiorów p=q:
Dwa zbiory p i q są tożsame p=q wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q (A1: p=>q=1) i jednocześnie zbiór q jest podzbiorem => zbioru p (B3: q=>p=1)
p=q <=> (A1: p=>q)*(B3: q=>p) = A1B3: p<=>q
Innymi słowy:
Tożsama definicja tożsamości zbiorów p=q:
Dwa zbiory p I q są tożsame p=q wtedy i tylko wtedy gdy znajdują się w relacji równoważności p<=>q
p=q <=> A1B3: p<=>q = (A1: p=>q)*(B3: q=>p)
Dla B3 zastosujmy prawo Tygryska:
B3: q=>p = B1: p~>q
Stąd mamy kolejną, tożsamą definicję tożsamości zbiorów p=q.
Tożsama definicja tożsamości zbiorów p=q:
Dwa zbiory p i q są tożsame p=q wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q (A1: p=>q=1) i jednocześnie zbiór p jest nadzbiorem ~> zbioru q (B1: p~>q=1)
p=q <=> (A1: p=>q)*(B1: p~>q) = A1B1: p<=>q
Na mocy prawa Słonia mamy kolejną, tożsamą definicję tożsamości zbiorów p=q.
Tożsama definicja tożsamości zbiorów p=q:
Dwa zbiory p i q są tożsame p=q wtedy i tylko wtedy gdy zajście p jest konieczne ~> (B1) i wystarczające => (A1) dla zajścia q
p=q <=> (A1: p=>q)*(B1: p~>q) = A1B1: p<=>q
Przykład:
Równoważność Pitagorasa dla trójkątów prostokątnych:
RA1B1:
Trójkąt jest prostokątny (TP) wtedy i tylko wtedy gdy zachodzi w nim suma kwadratów (SK)
TP<=>SK = (A1: TP=>SK)*(B1: TP~>SK) =1*1=1
Bycie trójkątem prostokątnym (TP) jest warunkiem koniecznym ~> (B1) i wystarczającym => (A1) to tego, aby zachodziła w nim suma kwadratów (SK)
Równoważność Pitagorasa udowadniamy w dwóch krokach.
Krok 1
Dowodzimy twierdzenia prostego Pitagorasa:
A1.
Jeśli trójkąt jest prostokątny to na 100% => zachodzi w nim suma kwadratów
TP=>SK =1
Twierdzenie proste Pitagorasa ludzkość udowodniła wieki temu
Dowód ten oznacza, że zbiór TP jest podzbiorem => zbioru SK
Krok 2
Prawdziwość warunku koniecznego (B1: TP~>SK) w równoważności Pitagorasa dowodzimy metodą „nie wprost”
Prawo Tygryska:
B1: TP~>SK = B3: SK=>TP
Na mocy prawa Tygryska aby udowodnić prawdziwość warunku koniecznego B1: TP~>SK potrzeba i wystarcza udowodnić prawdziwość twierdzenia odwrotnego Pitagorasa B3: SK=>TP
B3.
Jeśli w dowolnym trójkącie zachodzi suma kwadratów (SK) to ten trójkąt na 100% => jest prostokątny (TP)
SK=>TP =1
Twierdzenie odwrotne Pitagorasa ludzkość udowodniła wieki temu.
Dowód ten oznacza, iż zbiór SK jest podzbiorem => zbioru TP
Stąd dla naszego przykładu mamy:
Definicja tożsamości zbiorów TP=SK:
Dwa zbiory TP i SK są tożsame TP=SK wtedy i tylko wtedy gdy zbiór TP jest podzbiorem => zbioru SK (Twierdzenie proste A1: TP=>SK=1) i jednocześnie zbiór SK jest podzbiorem => zbioru TP (Twierdzenie odwrotna B3: SK=>TP=1)
TP=SK <=> (A1: TP=>SK)*(B3: SK=>TP) = A1B3: TP<=>SK
Wniosek:
Równoważność Pitagorasa dla trójkątów prostokątnych (TP<=>SK) definiuje tożsamość zbiorów TP=SK
cnd
Stąd mamy:
Prawo Irbisa dla zbiorów:
Dowolna równoważność prawdziwa p<=>q=1 definiuje tożsamość zbiorów p=q i odwrotnie
N6.2 Prawo Irbisa dla zdarzeń
Definicja tożsamości zdarzeń p=q:
Dwa zdarzenia p i q są tożsame p=q wtedy i tylko wtedy gdy zajście p jest konieczne ~> (B1) i wystarczające => (A1) dla zajścia q
Dowód na przykładzie:
| Kod: |
S1 Schemat ideowy sterowania żarówką
A<=>S = (A1: A=>S)*(B1: A~>S)=1*1=1
S A
------------- ______
-----| Żarówka |-------o o-----
| ------------- |
| |
______ |
___ U (źródło napięcia) |
| |
| |
------------------------------------
|
Wciśnięcie przycisku A (A=1) jest warunkiem koniecznym ~> (B1) i wystarczającym => (A1) do tego, aby żarówka świeciła się S (S=1)
A<=>S = (A1: A=>S)*(B1: A~>S)=1*1=1
Zachodzi tu tożsamość pojęć A=S:
A=S <=> (A1: A=>S)*(B1: A~>S) = A<=>S
Innymi słowy:
Pojęcie „przycisk A wciśnięty” jest tożsame z pojęciem „żarówka S świeci się”
Stąd mamy:
Prawo Irbisa:
Dowolna równoważność prawdziwa p<=>q=1 definiuje tożsamość zbiorów/zdarzeń p=q i odwrotnie
N7 Pozostałe znaczki w algebrze Kubusia
| Kod: |
T0
Fundament algebry Kubusia w obsłudze zdań warunkowych „Jeśli p to q”
Matematyczne związki warunku wystarczającego => i koniecznego ~>:
A1B1: A2B2: | A3B3: A4B4:
A: 1: p=>q = 2:~p~>~q [=] 3: q~>p = 4:~q=>~p [=] 5: ~p+q
## ## ## ## ##
B: 1: p~>q = 2:~p=>~q [=] 3: q=>p = 4:~q~>~p [=] 5: p+~q
Prawa Kubusia: | Prawa kontrapozycji dla warunku wystarczającego =>:
A1: p=>q = A2:~p~>~q | A1: p=>q = A4:~q=>~p
B1: p~>q = B2:~p=>~q | B2:~p=>~q = B3: q=>p
Prawa Tygryska: | Prawa kontrapozycji dla warunku koniecznego ~>:
A1: p=>q = A3: q~>p | A2:~p~>~q = A3: q~>p
B1: p~>q = B3: q=>p | B1: p~>q = B4:~q~>~p
Gdzie:
## - różne na mocy definicji warunku wystarczającego => i koniecznego ~>
p i q muszą być wszędzie tymi samymi p i q inaczej błąd podstawienia
|
N7.1 Implikacja prosta p|=>q
Implikacja prosta p|=>q:
A1: p=>q =1 - zajście p jest (=1) wystarczające => dla zajścia q
B1: p~>q =0 - zajście p nie jest (=0) konieczne ~> dla zajścia q
Stąd:
p|=>q = (A1: p=>q)*~(B1: p~>q)=1*~(0)=1*1=1
Czytamy:
Implikacja prosta p|=>q jest prawdziwa (=1) wtedy i tylko wtedy gdy zajście p jest (=1) wystarczające => dla zajścia q (A1) i nie jest (=0) konieczne ~> dla zajścia q
Inaczej:
p|=>q =0
Przykład:
A1.
Jeśli dowolna liczba jest podzielna przez 8 to na 100% => jest podzielna przez 2
P8=>P2=1
Podzielność dowolnej liczby przez 8 jest warunkiem wystarczającym => dla jej podzielności przez 2 bo zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8..]
cnd
Badamy warunek konieczny ~> między tymi samymi punktami i w tym samym kierunku
B1.
P8~>P2 =0 - bo zbiór P8=[8,16,24..] nie jest nadzbiorem ~> zbioru P2=[2,4,6,8..]
cnd
Stąd mamy rozstrzygnięcie iż oba zdania A1 i B1 wchodzą w skład implikacji prostej P8|=>P2:
P8|=>P2=(A1: P8=>P2)*(B1: P8~>P2) = 1*~(0)=1*1=1
Czytamy:
Podzielność dowolnej liczby przez 8 jest wystarczająca => dla jej podzielności przez 2 (A1) ale nie jest konieczna ~> (B1) dla jej podzielności przez 2
N7.2 Implikacja odwrotna p|~>q
Implikacja odwrotna p|~>q:
A1: p=>q =0 - zajście p nie jest (=0) wystarczające => dla zajścia q
B1: p~>q =1 - zajście p jest (=1) konieczne ~> dla zajścia q
Stąd:
p|~>q = ~(A1: p=>q)*(B1: p~>q)=~(0)*1=1*1=1
Czytamy:
Implikacja odwrotna p|~>q jest prawdziwa (=1) wtedy i tylko wtedy gdy zajście p jest (=1) konieczne ~> dla zajścia q (B1) i nie jest (=0) wystarczające => dla zajścia q (A1)
Przykład:
B1.
Jeśli dowolna liczba jest podzielna przez 2 to może być podzielna przez 8
P2~>P8 =1
Podzielność dowolnej liczby przez 2 jest (=1) warunkiem konicznym ~> dla jej podzielności przez 8 bo zbiór P2=[2,4,6,8..] jest nadzbiorem ~> zbioru P8=[8,16,24..]
Oczywiście tu można skorzystać z prawa Tygryska:
B1: P2~>P8 = B3: P8=>P2
i dowodzić łatwiejszy w dowodzeniu warunek wystarczający B3: P8=>P2
cnd
Badamy czy spełniony jest warunek wystarczający => między tymi samymi punktami i w tym samym kierunku.
A1.
Jeśli dowolna liczba jest podzielna przez 2 to na 100% => jest podzielna przez 8
P2=>P8 =0
Podzielność dowolnej liczby przez 2 nie jest warunkiem wystarczającym => dla jej podzielności przez 8 bo zbiór P2=[2,4,6,8..] nie jest podzbiorem => P8=[8,16,24..]
cnd
Stąd mamy rozstrzygnięcie, iż oba zdania A1 i B1 wchodzą w skład implikacji odwrotnej P2|~>P8:
P2|~>P8 = ~(A1: P2=>P8)*(B1: P2~>P8)=~(0)*1=1*1=1
Czytamy:
Podzielność dowolnej liczby przez 2 jest (=1) konieczna ~> (B1) dla jej podzielności przez 8, ale nie jest wystarczająca => (A1) dla jej podzielności przez 8
N7.3 Równoważność p<=>q
Definicja równoważności p<=>q:
A1: p=>q =1 - zajście p jest (=1) wystarczające => dla zajścia q
B1: p~>q =1 - zajście p jest (=1) konieczne ~> dla zajścia q
Stąd:
p<=>q = (A1: p=>q)*(B1: p=>q)=1*1=1
Czytamy:
Równoważność p<=>q jest prawdziwa (=1) wtedy i tylko wtedy gdy zajście p jest konieczne (B1) i wystarczające => (A1) dla zajścia q
Inaczej:
p<=>q =0
Przykład:
Równoważność Pitagorasa dla trójkątów prostokątnych:
Trójkąt jest prostokątny (TP) wtedy i tylko wtedy gdy zachodzi w nim suma kwadratów (SK)
TP<=>SK = (A1: TP=>SK)*(B1: TP~>SK) =1*1=1
Prawą stronę czytamy:
Bycie trójkątem prostokątnym (TP) jest warunkiem koniecznym ~> (B1) i wystarczającym => A1) do tego, aby zachodziła w nim suma kwadratów
N7.4 Spójnik „albo”($)
Definicja spójnika „albo”($):
A1: p=>~q =1 - zajście p jest (=1) wystarczające => dla zajścia ~q
B1: p~>~q =1 - zajście p jest (=1) konieczne ~> dla zajścia ~q
Stąd:
p$q = (A1: p=>~q)*(B1: p~>~q)=p<=>~q
Czytamy:
Spójnik „albo”($) jest spełniony (=1) wtedy i tylko wtedy gdy zajście p jest konieczne ~> (B1) i wystarczające => (A1) dla zajścia ~q
Przykład:
Dowolny człowiek jest mężczyzną (M) „albo”(+) kobietą (K)
M$K = (A1: M=>~K)*(B1: M~>~K)=M<=>~K
Zdanie matematycznie tożsame to odczyt prawej strony:
Dowolny człowiek jest mężczyzną (M) wtedy i tylko wtedy gdy nie jest kobietą (~K)
M<=>~K = (A1: M=>~K)*(B1: M~>~K) = M$K
Kolejne zdanie tożsame to odczyt środka:
Definicja spójnika „albo”($) jest spełniona (=1) wtedy i tylko wtedy gdy bycie mężczyzną (M) jest warunkiem koniecznym ~> (B1) i wystarczającym => (A1) do tego, by nie być kobietą
N7.5 Chaos p|~~>q
Definicja chaosu p|~~>q:
Chaos p|~~>q to nie zachodzenie ani warunku koniecznego ~> ani tez wystarczającego => miedzy tymi samymi punktami i w tym samym kierunku
A1: p=>q =0 - zajście p nie jest (=0) wystarczające => dla zajścia q
B1: p~>q =0 - zajście p nie jest (=0) konieczne ~> dla zajścia q
p|~~>q = ~(A1: p=>q)*~(B1: p~>q)=~(0)*~(0)=1*1=1
Przykład:
A.
Jeśli dowolna liczba jest podzielna przez 8 to może ~~> być podzielna przez 3
P8~~>P3 = P8*P3 =1
W operatorze chaosu P8|~~>P3 chodzi o to że nie może być warunku wystarczającego => między dowolnymi przeczeniami P8 i P3
Sprawdźmy:
| Kod: |
A: P8~~> P3= P8* P3=1 bo 24
B: P8~~>~P3= P8*~P3=1 bo 8
C:~P8~~>~P3=~P8*~P2=1 bo 1
D:~P8~~> P3=~P8* P3=1 bo 3
|
cnd
Ostatnio zmieniony przez rafal3006 dnia Pon 11:53, 28 Mar 2022, w całości zmieniany 5 razy
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39692
Przeczytał: 8 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Nie 21:54, 27 Mar 2022 Temat postu: Wysłany: Nie 21:54, 27 Mar 2022 Temat postu: |
|
|
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#653193
Czy Irbisol nawiąże sensowną dyskusję?
Czy Irbisol zgodzi się na króciutki wykład w temacie kiedy zdania podobne do tych z jego cytatu zaczną mieć sens, czyli zaczną opisywać operator implikacji prostej p||=>q
Czy ktoś ma nadzieję, że Irbisol odpowie:
Chcę!
Malunek z angielskiej Wikipedii przytoczony przez Irbisola jest następujący:
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1300.html#636141
| Irbisol napisał: |
W angielskiej Wikipedii masz:

Bycie w obszarze fioletowym jest wystarczające do bycia w A, ale nie jest konieczne. Bycie w A jest konieczne, aby znaleźć się w fioletowym regionie, ale nie wystarczy. Bycie w A i bycie w B jest konieczne i wystarczające, aby znaleźć się w fioletowym regionie
[link widoczny dla zalogowanych] |
| Irbisol napisał: | | rafal3006 napisał: | | Irbisol napisał: | | Nadal nie wiem, skąd ci przyszło do głowy, że malunek ma opisywać OR. |
Jak wszyscy widzą, Irbisola w ogóle nie interesuje dyskusja na temat JEGO malunku z Wikipedii!
Irbisol będzie teraz do końca świata powtarzał to zdanie wyżej, mimo iż napisałem mu w moich postach wyżej, że malunek z angielskiej Wikipedii nie pasuje do żadnego z sześciu możliwych operatorów logicznych - oczywiście wszystko mogę po kolei udowodnić. |
Ale ja nie twierdzę, że ten malunek opisuje którykolwiek z operatorów logicznych.
Pytam, skąd ci przyszło do głowy, że ten malunek ma na celu jakikolwiek opisywać.
Ty naprawdę nie rozumiesz najprostszych zdań i nie ma z tobą kontaktu. |
Jak wszyscy widzą, Irbisol będzie teraz w koło Macieju pisał to samo nie wyrażając zgody na mój króciutki wykład kiedy malunek z Wikipedii i opis pod nim będzie miał operatorowy sens.
Co do wytłuszczonego:
Bezdyskusyjnie malunek z Wkipedii poprawnie pokazuje definicję spójnika „lub”(+):
Y = p+q
co udowodniłem w tym poście:
http://www.sfinia.fora.pl/filozofia,4/algebra-kubusia-rewolucja-w-logice-matematycznej,16435-1600.html#652939
… ale wtedy ten opis pod rysunkiem jest gównem, nie mającym związku z opisem spójnika „lub”(+):
Y=p+q
cnd
Dokładnie dlatego opis ten jest tylko i wyłącznie u angielskiego matoła, autora wpisu do Wikipedii, nie mającego pojęcia o logice matematycznej.
Istnieją precyzyjne malunki, nieznane ziemskim matematykom, opisując wszystkie 6 operatorów logicznych występujących w logice matematycznej.
Moje pytanie jest następujące:
Czy chcesz poznać poprawną interpretację w zbiorach operatora implikacji prostej p||=>q - tu opis z Wikipedii jest prawie dobry z małym wyjątkiem.
Moje pytanie brzmi:
Czy chcesz poznać ten mały wyjątek, po uwzględnieniu którego malunek i opis z Wikipedii będzie pasował do opisu operatora implikacji prostej p||=>q?
Czy ktokolwiek ma nadzieję, że Irbisol napisze:
Chcę!
Ostatnio zmieniony przez rafal3006 dnia Nie 22:02, 27 Mar 2022, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
|
|
Nie możesz pisać nowych tematów
Nie możesz odpowiadać w tematach
Nie możesz zmieniać swoich postów
Nie możesz usuwać swoich postów
Nie możesz głosować w ankietach
|
fora.pl - załóż własne forum dyskusyjne za darmo
Powered by phpBB © 2001, 2005 phpBB Group
|






