 |
ŚFiNiA
ŚFiNiA - Światopoglądowe, Filozoficzne, Naukowe i Artystyczne forum - bez cenzury, regulamin promuje racjonalną i rzeczową dyskusję i ułatwia ucinanie demagogii. Forum założone przez Wuja Zbója.
|
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 12:21, 14 Mar 2016 Temat postu: Wysłany: Pon 12:21, 14 Mar 2016 Temat postu: |
|
|
Jak zwykle:
Z dedykacją dla Komandora, Czarnej Mańki i Pana Baryckiego
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-375.html#272968
Algebra Kubusia
Nowa Teoria Zbiorów
Część II
Link do części I
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-375.html#271848
| fiklit napisał: |
Jak tam obalanie diagramów? |
Dzięki za diagram, dobrze idzie … 

Podstawiam klasykę:
p=S
q=P
… by być w zgodzie z ogólnie przyjętymi symbolami w zapisach formalnych (ogólnych) - tylko i wyłącznie po to!
Powyższe diagramy są w 100-milowym lesie znane od zawsze, zatem to żadna nowość.
Zauważmy, że diagramy ziemian są niechlujnie narysowane bo wszystkich możliwych iloczynów logicznych dla dwóch zbiorów S i P jest:
od dwóch w równoważności do czterech w operatorze chaosu (ziemska niezależność)
… tymczasem np. w „niezależności” ziemian mamy pięć niezależnych iloczynów logicznych.
Oto one:
| Kod: |
Niezależność - iloczyny logiczne zbiorów od strony lewej do prawej
A: ~S*~P =1
B: S*~P =1
C: S* P =1
D: ~S* P =1
E: ~S*~P =1
|
Linie A i E są matematycznie tożsame, zatem jedną z nich możemy posłać w kosmos.
Formalnie „niezależność” Ziemian jest dobrze przedstawiona na diagramie, co nie zmienia faktu iż jest to najzwyklejsze niechlujstwo. Analogią może tu być tabliczka mnożenia do 100 zawierająca wszystkie możliwe mnożenia plus dowolną ilość powtórzeń (formalnie to jest dozwolone) - tego typu matematyczny bałagan dobry nauczyciel matematyki powinien tępić.
Dokładnie to samo co wyżej w algebrze Kubusia!

Wstęp teoretyczny, fragment dekalogu Nowej Teorii Zbiorów:
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-375.html#271848
Zacytujmy najważniejsze, 10 przykazanie:
| Kubuś napisał: |
10.
Definicja kontrprzykładu w zbiorach
Definicja warunku wystarczającego => w zbiorach:
A.
Jeśli zajdzie p to na pewno => zajdzie q
p=>q
Warunek wystarczający p=>q =1 jest spełniony (=1) wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q (Inaczej: p=>q =0)
Prawdziwość warunku wystarczającego A gwarantuje fałszywość kontrprzykładu B (i odwrotnie)
B.
Jeśli zajdzie p to może ~~> zajść ~q
p~~>~q = p*~q
Kwantyfikator mały p~~>~q =1 jest spełniony (=1) gdy istnieje wspólny element zbiorów p*~q (Inaczej: p~~>~q =0)
Definicja kontrprzykładu w zbiorach:
Kontrprzykładem dla warunku wystarczającego p=>q nazywamy to samo zdanie z zanegowanym następnikiem kodowane kwantyfikatorem małym p~~>~q =p*~q
Rozstrzygnięcia:
10-1.
Prawdziwość kontrprzykładu p~~>~q =p*~q =1 daje nam gwarancję matematyczną fałszywości zdania kodowanego warunkiem wystarczającym p=>q =0 (i odwrotnie)
10-2.
Fałszywość kontrprzykładu p~~>~q =p*~q =0 daje nam gwarancję matematyczną prawdziwości warunku wystarczającego p=>q=1 (i odwrotnie) |
Poprawne diagramy wszystkich możliwych wzajemnych położeń zbiorów p i q
1.
Implikacji prosta p|=>q (ziemska „podrzędność”)
Dowód:

Definicja implikacji prostej p|=>q:
Zbiór p jest podzbiorem => zbioru q i nie jest tożsamy ze zbiorem q
p|=>q = (p=>q)*~[p=q]
Doskonale to widać w diagramie wyżej.
Wyprowadzenie symbolicznej definicji implikacji prostej p|=>q.
Zapiszmy wszystkie możliwe iloczyny logiczne występujących tu zbiorów:
| Kod: |
A: p* q =1
B: p*~q =0
C: ~p*~q =1
D: ~p* q =1 |
Oczywistym jest, że kolejność zapisanych linii jest bez znaczenia.
Definicja implikacji w zbiorach:
Implikacja to trzy i tylko trzy zbiory niepuste i rozłączne w obrębie dziedziny (A,C i D)
p|=>q = A: p*q + C:~p*~q + D: ~p*q
Dla naszych zbiorów A i B korzystamy z przykazania 10-2 NTZ otrzymując:
| Kod: |
A: p=> q =1
B: p~~>~q =0
|
Z założenia (diagram podrzędności) zbiór p musi być podzbiorem zbioru q oraz zbiory p i q nie są tożsame (również z założenia podrzędności).
Wynika z tego ze zbiór ~p musi być nadzbiorem ~> zbioru ~q.
Stąd mamy pełną, symboliczną tabelę prawdy dla implikacji prostej p|=>q (zwanej u ziemian podrzędnością).
| Kod: |
p|=>q
A: p=> q =1 - bo zbiór p jest podzbiorem => zbioru q
B: p~~>~q=0 - bo zbiory p i ~q są rozłączne
C:~p~>~q =1 - bo zbiór ~p jest nadzbiorem ~> zbioru ~q
lub
D:~p~~>q =1 - bo istnieje część wspólna zbiorów ~p i q
|
Zauważmy, że:
Jeśli zajdzie p to mamy gwarancję matematyczną => iż zajdzie q (bo linia B jest fałszem).
Linie A i B realizują 100% pewność matematyczną, nieodzowny element każdej implikacji.
Jeśli natomiast zajdzie ~p to może ~> się zdarzyć że zajdzie ~q (linia C) lub może ~~> się zdarzyć że zajdzie q (linia D).
Linie C i D to najzwyklejsze „rzucanie monetą” drugi fundament każdej implikacji rzeczywistej!
Algorytm wyprowadzenia tabeli prawdy dla dowolnego diagramu jest identyczny jak przedstawiony wyżej, zawsze zaczynamy od wynikowych zer w zbiorach lokalizując warunki wystarczające => i konieczne ~> w tabeli prawdy.
Wniosek:
Ziemska „podrzędność” to nic innego jak symboliczna definicja implikacji prostej p|=>q
To są nieprawdopodobne banały czysto matematyczne jak to przedstawiono na przykładzie ziemskiej podrzędności.
Nie będę tych banałów w kółko powtarzał wierząc, iż nawet Idiota potrafi je zrozumieć.
Prawda Idioto?
Podsumowanie:
Definicja implikacji prostej |=> (podrzędności u ziemian):
Zbiór p jest podzbiorem => q i nie jest tożsamy ze zbiorem q
p|=>q = (p=>q)*~[p=q]
Pełna definicja symboliczna implikacji prostej p|=>q
| Kod: |
p|=>q
A: p=> q =1 - bo zbiór p jest podzbiorem => zbioru q
B: p~~>~q=0 - bo zbiory p i ~q są rozłączne
C:~p~>~q =1 - bo zbiór ~p jest nadzbiorem ~> zbioru ~q
lub
D:~p~~>q =1 - bo istnieje część wspólna zbiorów ~p i q
|
Zauważmy, że definicja implikacji prostej p|=>q wymusza nam matematyczny związek między warunkiem wystarczającym => i koniecznym ~>.
Prawo Kubusia:
Jeśli zbiór p jest podzbiorem => zbioru q to mamy gwarancję matematyczną iż zbiór ~p jest nadzbiorem ~> zbioru ~q (i odwrotnie)
p=>q = ~p~>~q
Prawo Kubusia to tożsamość „=” logiczna będąca de facto równoważnością.
Tożsamość logiczna ma wszystkie cechy klasycznej tożsamości.
Zauważmy, że w prawie Kubusia nie ma znaczenia czy zbiory p i q nie są tożsame (~[p=q] - implikacja), czy też są tożsame ([p=q] - równoważność)
Zdanie A to wyłącznie warunek wystarczający p=>q wchodzący w skład definicji implikacji prostej p|=>q.
Implikacja prosta p|=>q to seria czterech zdań A,B,C i D a nie jedno zdanie.
Przykład:
A.
Jeśli liczba jest podzielna przez 8 to na pewno => jest podzielna przez 2
P8=>P2 =1
Definicja warunku wystarczającego => spełniona bo:
Zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8 ..]
Dodatkowo zbiory P8 i P2 nie są tożsame co wymusza definicję implikacji prostej P8|=>P2:
P8|=>P2 = (P8=>P2)*~[P8=P2]
Dalszą analizę matematyczną wykona najgłupszy komputer.
Tabela prawdy dla naszego zadnia A jest następująca:
| Kod: |
P8|=>P2
A: P8=> P2 =1 - bo P8=[8,16,24..] jest podzbiorem => P2=[2,,4,6,8..]
B: P8~~>~P2=0 - bo zbiory P8=[8,16,24..] i ~P2=[1,3,5,7..] są rozłączne
C:~P8~>~P2 =1 - bo ~P8=[1,2,3,4,5,6,7..9.] jest nadzbiorem ~> ~P2=[1,3,5..]
D:~P8~~>P2 =1 - bo ~P8=[1,2,3,4,5,6,7..9.] ma część wspólną ~~> z P2=[2,4.]
|
Zdanie A nie jest implikacją prostą P8=>P2, jak to błędnie bredzą ziemianie.
Zdanie A to wyłącznie warunek wystarczający P8=>P2 wchodzący w skład definicji implikacji prostej P8|=>P2.
Implikacja prosta P8|=>P2 to seria czterech zdań A,B,C i D a nie jedno zdanie.
2.
Implikacji odwrotna p|~>q (ziemska „nadrzędność”)

Definicja implikacji odwrotnej p|~>q:
Zbiór p jest nadzbiorem ~> zbioru q i nie jest tożsamy ze zbiorem q
p|~>q = (p~>q)*~[p=q]
Doskonale to widać na diagramie wyżej.
Wyprowadzenie symbolicznej definicji implikacji odwrotnej:
Na początek zapisujemy wszystkie możliwe iloczyny logiczne zbiorów tu występujących.
| Kod: |
Symboliczne definicja implikacji odwrotnej w spójnikach „i”(*) i „lub”(+)
A: p* q =1
B: p*~q =1
C:~p*~q =1 | ~p=>~q =1 - na mocy 10-2 przykazania NTZ
D:~p* q =0 | ~p~~>q =0
|
Definicja implikacji w zbiorach:
Implikacja to trzy i tylko trzy zbiory niepuste i rozłączne w obrębie dziedziny (A, B i C)
Nasz przykład:
D = A: p*q + B: p*~q + C: ~p*~q
Korzystając z przykazania 10-2 NTZ lokalizujemy występujący tu warunek wystarczający w linii C, jak to pokazano wyżej.
Na mocy prawa Kubusia warunek wystarczający => w linii C wymusza warunek konieczny ~> w linii A, niezależnie od tego czy zbiory p i q nie są tożsame (~[p=q] - implikacja), czy też są tożsame ([p=q] - równoważność).
Prawo Kubusia:
C: ~p=>~q = A: p~>q
Stąd mamy końcową tabelę symboliczną implikacji odwrotnej p|~>q.
| Kod: |
Symboliczna definicja implikacji odwrotnej p|~>q w spójnikach =>,~>,~~>
A: p~> q =1 - bo zbiór p jest nadzbiorem ~> zbioru q
lub
B: p~~>~q=1 - bo istnieje wspólny element zbiorów p i ~q
C:~p=>~q =1 - bo zbiór ~p jest podzbiorem => zbioru ~q
D:~p~~>q =0 - bo zbiory ~p i q mają część wspólną
|
Zauważmy, że w implikacji odwrotnej p|~>q po stronie p mamy „rzucanie monetą” natomiast gwarancję matematyczną => mamy po stronie ~p.
Rzucanie monetą:
Jeśli zajdzie p to może ~> zajść q (zdanie A) lub jeśli zajdzie p to może ~~> zajść ~q (zdanie B).
Czyli:
Jeśli zajdzie p to wszystko może się zdarzyć, może ~> zajść q lub może zajść ~q - mamy najzwyklejsze „rzucanie monetą”
Gwarancja matematyczna w implikacji odwrotnej p|~>q:
Jeśli zajdzie ~p to mamy gwarancję matematyczną => iż zajdzie ~q (bo linia D jest fałszem).
Linie C i D realizują 100% pewność matematyczną, nieodzowny element każdej implikacji.
Zdanie A to warunek konieczny p~>q wchodzący w skład definicji implikacji odwrotnej p|~>q.
Implikacja odwrotna p|~>q to seria czterech zdań A,B,C i D a nie jedno zdanie.
Przykład:
A.
Jeśli liczba jest podzielna przez 2 to może ~> być podzielna przez 8
P2~>P8 =1
Definicja warunku koniecznego ~> spełniona bo:
Zbiór P2=[2,4,6,8..] jest nadzbiorem ~> zbioru P8=[8,16,24..]
Dodatkowo zbiory P2 i P8 nie są tożsame co wymusza definicję implikacji odwrotnej P2|~>P8:
P2|~>P8 = (P2~>P8)*~[P2=P8]
Dalszą analizę potrafi wykonać najgłupszy komputer.
| Kod: |
Symboliczna definicja implikacji odwrotnej p|~>q w spójnikach =>, ~> i ~~>
P2|~>P8
A: P2~> P8 =1 -bo P2=[2,4,6,8.] jest nadzbiorem ~> P8=[8,16,24..]
B: P2~~>~P8=1 -bo istnieje wspólny element zbiorów P2=[2,4,6.] i ~P8=[1,2.]
C:~P2=>~P8 =1 -bo ~P2=[1,3,5.] jest podzbiorem => ~P8=[1,2,3,4,5,6,7..9.]
D:~P2=> P8 =0 -bo zbiory ~P2=[1,3,5..] i P8=8,16,24..] są rozłączne
|
Zdanie A to warunek konieczny P2~>P8 wchodzący w skład definicji implikacji odwrotnej P2|~>P8.
Implikacja odwrotna P2|~>P8 to seria czterech zdań A,B,C i D a nie jedno zdanie.
3.
Równoważność = diagram równoważności p<=>q

Definicja równoważności p<=>q:
Zbiór p jest podzbiorem => zbioru q i jest tożsamy ze zbiorem q
p<=>q = (p=>q)*[p=q]
Doskonale to widać na diagramie.
Wyprowadzenie symbolicznej definicji równoważności <=>.
Wszystkie możliwe iloczyny logiczne zbiorów odczytane z diagramu:
| Kod: |
A: p* q =1
B: p*~q =0
C: ~p*~q =1
D: ~p* q =0 |
Definicja równoważności w zbiorach:
Równoważność to dwa i tylko dwa zbiory niepuste i rozłączne w obrębie dziedziny (A i C):
p<=>q = A: p*q + C: ~p*~q
Korzystamy z przykazania 10-2 Nowej Teorii Zbiorów, otrzymując banalną definicję symboliczną równoważności p<=>q
| Kod: |
Definicja równoważności p<=>q w spójnikach =>, ~> i ~~>
p<=>q
A: p=> q =1 - bo zbiór p jest podzbiorem => q
B: p~~>~q=0 - bo zbiory p i ~q są rozłączne
C:~p=>~q =1 - bo zbiór ~p jest podzbiorem => ~q
D:~p~~>q =0 - bo zbiory ~p i q są rozłączne
|
Porównajmy diagram równoważności p<=>q z diagramami implikacji prostej p|=>q i odwrotnej p|~>q.

Klasyczna równoważność to tożsamość zbiorów [p=q] wymuszająca tożsamość zbiorów [~p=~q]
Prawo Morsa:
Dowolna tożsamość (także z matematyki klasycznej) to automatycznie równoważność
Przykład:
pies=pies
pies<=>pies = (pies=>pies)*(~pies=>~pies)
2=2
2<=>2 = (2=>2)*(~2=>~2)
itd
R1.
Definicja tożsamości zbiorów p i q (uwielbiana przez matematyków):
Zbiór p jest tożsamy ze zbiorem q wtedy i tylko wtedy gdy każdy element zbioru p należy do zbioru q i odwrotnie
R1: p<=>q = (p=>q)*(q=>p)
R2.
Tożsama definicja tożsamości zbiorów p i q:
Zbiór p jest tożsamy ze zbiorem q wtedy i tylko wtedy gdy każdy element zbioru p należy do zbioru q i każdy element zbioru ~p należy do zbioru ~q
R2: p<=>q = (p=>q)*(~p=>~q)
R3.
Kolejna tożsama definicja tożsamości zbiorów p i q:
Zbiór p jest tożsamy ze zbiorem q wtedy i tylko wtedy gdy zachodzą jednocześnie warunek wystarczający p=>q i konieczny p~>q między tymi samymi punktami:
R3: p<=>q = (p=>q)*(p~>q)
Doskonale widać, że wyłącznie w przypadku tożsamości zbiorów spełniony jest jednocześnie warunek wystarczający p=>q i konieczny p~>q między tymi samymi punktami.
To są trzy najważniejsze definicje równoważności (tożsamości zbiorów), spotykane w praktyce.
Zapiszmy aktualnie wyprowadzone definicje tożsamości zbiorów p=q jedne pod drugą:
R1: p<=>q = (p=>q)*(q=>p)
R2: p<=>q = (p=>q)*(~p=>~q)
R3: p<=>q = (p=>q)*(p~>q)
Kolejne, trywialne definicje tożsamości zbiorów p=q i ~p=~q wynikłe z teorii zbiorów to:
R4: p<=>q = (q=>p)*(~q=>~p) - definicja symetryczna do R2
etc
Dalsze definicje możemy tworzyć korzystając z naturalnej logiki matematycznej każdego człowieka jak to uczyniliśmy w definicjach R1,R2,R3 i R4.
Możemy też korzystać do woli z praw Kubusia które obowiązują zarówno w równoważności, jak i w implikacji.
Prawa Kubusia:
p=>q = ~p~>~q
p~>q = ~p=>~q
Zabawę w dalsze generowanie tożsamych definicji równoważności pozostawiam czytelnikowi.
Z R1 i R4 mamy prawo kontrapozycji poprawne w równoważności (i tylko tu!):
p=>q = ~q=>~p
W twierdzeniach matematycznych będących z definicji warunkiem wystarczającym p=>q po udowodnieniu prawdziwości tego warunku p=>q=1, matematycznie możemy założyć cokolwiek np. że nasz udowodniony warunek wystarczający p=>q wchodzi w skład definicji równoważności.
p<=>q = (p=>q)*(q=>p) =1*1 =1
Dopiero po udowodnieniu twierdzenia odwrotnego q=>p =1 mamy pewność, że nasze twierdzenie proste p=>q wchodzi w skład definicji równoważności, inaczej nasze twierdzenie proste p=>q to tylko warunek wystarczający p=>q wchodzący w skład definicji implikacji prostej p|=>q.
Definicja implikacji prostej |=>:
Zbiór p jest podzbiorem => zbioru q i nie jest tożsamy ze zbiorem q
p|=>q = (p=>q)*~[p=q]
Przykład:
A.
Jeśli trójkąt jest prostokątny to na pewno => zachodzi suma kwadratów
TP=>SK =1
Definicja warunku wystarczającego => spełniona bowiem zbiór TP jest podzbiorem zbioru SK
Dodatkowo zbiory TP i SK są tożsame, co wymusza definicję równoważności TP<=>SK.
Dalszą analizę przez wszystkie możliwe przeczenia TP i SK potrafi zrobić byle komputer.
| Kod: |
TP<=>SK
A: TP=> SK =1 - bo zbiór TP jest podzbiorem => zbioru SK
B: TP~~>~SK=0 - bo zbiory TP i ~SK są rozłączne
C:~TP=>~SK =1 - bo zbiór ~TP jest podzbiorem => zbioru ~SK
D:~TP~~>SK =0 - bo zbiory ~TP i SK są rozłączne
|
Definicja równoważności:
Równoważność to jednoczesne zachodzenie warunku wystarczającego TP=>SK w logice dodatniej (bo SK) i warunku wystarczającego ~TP=>~SK w logice ujemnej (bo ~SK).
Trójkąt jest prostokątny wtedy i tylko wtedy gdy zachodzi suma kwadratów
TP<=>SK = (TP=>SK)*(~TP=>~SK)
Równoważność mówi nie tylko o tym co się dzieje po stronie zbioru TP<=>SK ale również odpowiada na pytanie co się dzieje w fundamentalnie innym zbiorze, w zbiorze trójkątów nieprostokątnych.
Trójkąt jest nieprostokątny wtedy i tylko wtedy gdy nie zachodzi suma kwadratów
~TP<=>~SK = (~TP=>~SK)*(TP=>SK)
4.
Operator chaosu = ziemska niezależność
Definicja operatora chaosu w zbiorach:

Zapiszmy iloczyny logiczne wszystkich możliwych zbiorów:
| Kod: |
A: p* q =1 - zbiory p i q mają część wspólną
B: p*~q =1 - zbiory p i ~q mają część wspólną
C:~p*~q =1 - zbiory ~p i ~q mają część wspólną
D:~p* q =1 - zbiory ~p i q mają część wspólną
|
Definicja operatora chaosu w zbiorach:
Operator chaosu to cztery i tylko cztery zbiory niepuste i rozłączne w obrębie dziedziny (A,B,C i D):
p|~~>q = A: p*q + B: p*~q + C: ~p*~q + D: ~p*q
Zauważmy, że w kolumnie wynikowej mamy same jedynki, zatem nie występuje tu ani warunek wystarczający =>, ani konieczny ~>.
Mamy tu do czynienia z totalną przypadkowością (z rzucaniem monetą), czyli z chaosem.
Operator chaosu w spójnikach implikacyjnych: =>, ~> i ~~>
| Kod: |
p|~~>q
A: p~~> q =1
B: p~~>~q =1
C:~p~~>~q =1
D:~p~~>q =1
|
Operator chaosu to wszystkie cztery linie A, B, C i D a nie którakolwiek jedna.
Przykład:
A.
Jeśli liczba jest podzielna przez 8 to może ~~> być podzielna przez 3
P8~~>P3 = P8*P3 =1 bo 24
Analiza matematyczna przez wszystkie możliwe przeczenia p i q.
| Kod: |
P8|~~>P3
A: P8~~> P3 = P8* P3 =1 bo 24
B: P8~~>~P3 = P8*~P3 =1 bo 8
C:~P8~~>~P3 =~P8*~P3 =1 bo 2
D:~P8~~> P3 =~P8* P3 =1 bo 3
|
5.
Nietypowa implikacja prosta ~p|=>q w logice dodatniej (bo q) = ziemskie podprzeciwieństwo

Zapiszmy wszystkie możliwe iloczyny logiczne zbiorów tu występujące:
| Kod: |
A: ~p* q =1
B: ~p*~q =0
C: p*~q =1
D: p* q =1
|
Korzystając z przykazania 10-2 Nowej Teorii Zbiorów lokalizujemy warunek wystarczający => i konieczny ~> tu występujący.
| Kod: |
A: ~p=> q =1 - bo zbiór ~p jest podzbiorem => q
B: ~p~~>~q=0 - bo zbiory ~p i ~q są rozłączne
C: p~>~q =1 - bo zbiór p jest nadzbiorem ~> zbioru ~q
D: p~~>q =1 - bo zbiory p i q mają część wspólną
|
Zauważmy, że:
Jeśli zajdzie ~p to mamy gwarancję matematyczną => iż zajdzie q (bo linia B jest fałszem).
Linie A i B realizują 100% pewność matematyczną, nieodzowny element każdej implikacji.
Jeśli natomiast zajdzie p to może ~> się zdarzyć że zajdzie ~q (linia C) lub może ~~> się zdarzyć że zajdzie q (linia D).
Linie C i D to najzwyklejsze „rzucanie monetą” drugi fundament każdej implikacji rzeczywistej!
Definicja obietnicy:
Jeśli dowolny warunek to nagroda
W=>N
Spełnienie warunku W jest warunkiem wystarczającym => dla otrzymania nagrody N
Obietnica to implikacja prosta W|=>N na mocy definicji, w tym przypadku nic nie musimy udowadniać.
Przykład:
A.
Jeśli nie ubrudzisz spodni to dostaniesz czekoladę
~B=> C =1
Czyste spodnie (~B=1) dają nam gwarancję matematyczną => otrzymania czekolady
Zdanie A to na mocy definicji implikacja prosta ~B|=>C:
Zajście zdarzenia ~B=1 jest wystarczające => dla zajścia C=1 i nie jest tożsame z C
~B|=>C = (~B=>C)*~[~B=C]
W tym momencie tabelę prawdy dla zdania A potrafi zapisać byle komputer.
| Kod: |
~B|=>C
A: ~B=> C =1 -czyste spodnie (~B=1) gwarantują => czekoladę (C=1)
B: ~B~~>~C=~B*~C=0 -zakaz złamania obietnicy A (~B*~C=0)
C: B~>~C =1 -Jeśli brudne spodnie (B=1) to możesz nie dostać czekolady (~C=1)
lub
D: B~~>C =~B* C=1 -Jeśli brudne spodnie (B=1) to możesz ~~> dostać czekoladę (C=1)
|
W świecie żywym (nie tylko u człowieka!) zdanie D to matematyczne prawo nadawcy do wręczenia nagrody mimo że odbiorca nie spełnił warunku nagrody.
6.
Nietypowa implikacja prosta p|=>~q w logice ujemnej (bo ~q) = ziemskie przeciwieństwo

Zapiszmy wszystkie możliwe iloczyny logiczne zbiorów tu występujące:
| Kod: |
A: p*~q =1
B: p* q =0
C: ~p* q =1
D: ~p*~q =1
|
Korzystając z przykazania 10-2 Nowej Teorii Zbiorów lokalizujemy warunek wystarczający => i konieczny ~> tu występujący.
| Kod: |
A: p=>~q =1 - bo zbiór p jest podzbiorem => ~q
B: p~~>q =0 - bo zbiory p i q są rozłączne
C: ~p~> q =1 - bo zbiór ~p jest nadzbiorem ~> zbioru q
lub
D: ~p~~>~q=1 - bo zbiory ~p i ~q mają część wspólną
|
Zauważmy, że:
Jeśli zajdzie p to mamy gwarancję matematyczną => iż zajdzie ~q (bo linia B jest fałszem).
Linie A i B realizują 100% pewność matematyczną, nieodzowny element każdej implikacji.
Jeśli natomiast zajdzie ~p to może ~> się zdarzyć że zajdzie q (linia C) lub może ~~> się zdarzyć że zajdzie ~q (linia D).
Linie C i D to najzwyklejsze „rzucanie monetą” drugi fundament każdej implikacji rzeczywistej!
Przykład:
Jeśli zwierzę jest psem to na pewno => nie jest kotem
P=>~K =1
Dziedzina:
ZWZ - zbiór wszystkich zwierząt
P=[pies]
K=[kot]
~K=[ZWZ-Kot] = [koń, kura, mrówka ..] - dowolne zwierzę z wykluczeniem kota
Definicja warunku wystarczającego => spełniona bo:
Zbiór P=[pies] jest podzbiorem zbioru ~K=[ZWZ-Kot]
Dodatkowo zbiór P=[pies] nie jest tożsamy ze zbiorem ~K=[ZWZ-Kot] co wymusza definicję implikacji prostej P|=>~K:
P|=>~K = (P=>~K)*~[P=~K]
Dalszą analizę przez wszystkie możliwe przeczenia P i ~K potrafi wykonać każdy przyzwoity komputer.
| Kod: |
A: P=> ~K =1 - bo zbiór „pies” jest podzbiorem => zbioru ~K=[ZWZ-Kot]
B: P~~>K = P*K =0 - bo zbiory „pies” i „kot” są rozłączne
C:~P~> K =1 - bo zbiór ~P=[ZWZ-Pies] jest nadzbiorem ~> K=[Kot]
lub
D:~P~~>~K=~P*~K=1 - bo zbiory ~P=[ZWZ-pies] i ~K=[ZWZ-Kot] mają część wspólną np. Kura
|
Zauważmy, że jeśli wylosujemy psa to w linii A mamy gwarancję matematyczną => iż na pewno nie będzie to kot.
Jeśli wylosujemy „nie psa” to w liniach C i D mamy najzwyklejsze rzucanie monetą, to może ~> być kot (zdanie C) lub nie kot (zdanie D).
7.
Prawo rozpoznawalności pojęcia p (prawo tożsamości wiedzy) = ziemska „sprzeczność”

Na mocy definicji:
Dwa zbiory niepuste p i ~p i rozłączne uzupełniające się wzajemnie do dziedziny oznaczają iż mamy do czynienia z równoważnością.
p+~p =1 (dziedzina)
p*~p =0
Analiza szczegółowa prawa rozpoznawalności wiedzy (prawa rozpoznawalności pojęcia p):
A.
Jeśli wiem co to jest p to na pewno => wiem co to jest ~p
p=>~p =1
Znajomość pojęcia p jest warunkiem wystarczającym => dla znajomości pojęcia ~p
B.
Jeśli wiem co to jest p to mogę ~~> nie wiedzieć co to jest p
p~~>~p =0 - nie ma takiej możliwości
C.
Jeśli wiem co to jest ~p to na pewno => wiem co to jest p
~p=>p =1
Znajomość pojęcia ~p jest warunkiem wystarczającym => dla znajomości pojęcia p
D.
Jeśli wiem co to jest ~p to mogę ~~> nie wiedzieć co to jest ~p
~p~~>~p =0 - nie ma takiej możliwości
Stąd mamy tabelę prawdy dla prawa rozpoznawalności pojęcia, tabelę równoważności:
| Kod: |
p<=>~p=(p=>~p)*(~p=>p)
A: p=>~p =1
B: p~~>p =0
C:~p=> p =1
D:~p~~>~p=0
|
Przykład 1
A.
Jeśli wiem co to jest „kolor biały” to na pewno wiem co to jest „kolor nie biały”
B=>~B =1
Dziedzina:
ZWK - zbiór wszystkich możliwych kolorów
Wiedza iż coś jest w kolorze białym jest warunkiem wystarczającym => na to by wiedzieć co to jest kolor „nie biały”
Gdzie:
„nie biały” - dowolny inny kolor niż biały
~B=[ZWK-biały] = [czarny, czerwony, zielony …] - zbiór wszystkich kolorów z wykluczeniem białego
Oczywistym jest że warunkiem koniecznym ~> i wystarczającym => dla rozpoznawalności koloru „biały” jest istnienie co najmniej jednego koloru „nie białego”
Stąd na mocy definicji równoważności mamy:
Kolor „nie biały” jest rozpoznawalny wtedy i tylko wtedy gdy rozpoznawalny jest kolor „biały”
~B<=>B = (~B~>B)*(~B=>B)
Przykład 2
A.
Jeśli znam dowolną funkcję logiczną Y to na pewno => znam funkcję ~Y
Y=>~Y =1
Znajomość funkcji Y jest warunkiem wystarczającym => dla znajomości funkcji ~Y
B.
Jeśli znam dowolną funkcję logiczną ~Y to na pewno => znam funkcję Y
~Y=>Y =1
Znajomość funkcji logicznej ~Y jest warunkiem wystarczającym => dla znajomości funkcji Y
Stąd mamy prawo rozpoznawalności funkcji logicznej Y:
Funkcja logiczna Y jest rozpoznawalna wtedy i tylko wtedy gdy rozpoznawalna jest funkcja logiczna ~Y
Y<=>~Y=(Y=>~Y)*(~Y=>Y) =1*1 =1
Przykład
Załóżmy że znamy funkcję logiczną:
Y=p+q - funkcja logiczna w logice dodatniej (bo Y)
Prawo przejścia do logiki przeciwnej:
Negujemy zmienne i wymieniamy spójniki na przeciwne
~Y=~p*~q - funkcja logiczna w logice ujemnej (bo ~Y)
Oczywistym jest że jeśli nie znamy funkcji logicznej Y:
Y=?
to automatycznie nie znamy funkcji logicznej ~Y
~Y=~?
Prawo tożsamości wiedzy znane jest wszystkim 5-cio latkom, czego dowód w tym poście:
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-325.html#271334
Gdzie mali inżynierowie (oboje po 5 wiosenek) Zuzia i Jaś zaprojektowali najprawdziwsze sterowanie windą w logice dodatniej (bo Y) oraz niezależnie, w logice ujemnej (bo ~Y).
Dziwne jest że ziemscy matematycy, nie mają bladego pojęcia o tym zdecydowanie najważniejszym prawie matematycznym naszego Wszechświata.
Ile jeszcze wody w Wiśle musi upłynąć, aby wiedza matematyczna ziemskiego matematyka dorównała do wiedzy każdego 5-cio latka i humanisty?
| idiota napisał: | | chyba obalone,amy nie zauważyliśmy... |
Idioto,
Kiedy twój biedny móżdżek, wyprany z naturalnej logiki matematycznej każdego człowieka, zrozumie najważniejsze prawo matematyczne naszego Wszechświata, prawo tożsamości wiedzy?
… doskonale znane każdemu 5-cio latkowi i humaniście!
Dowód:
Idiota do córci lat 5:
A.
Jutro pójdziemy do kina lub do teatru
Y=K+T
co matematycznie oznacza:
Y=1 <=> K=1 lub T=1
Czytamy:
Prawdą jest (=1), że dotrzymam słowa (Y) wtedy i tylko wtedy gdy JUTRO pójdziemy do kina (K=1) lub pójdziemy do teatru (T=1)
Córcia:
Tata, kiedy zostaniesz (w przyszłości) kłamcą?
Idiota:
Nie wiem córcia będę ci mógł powiedzieć czy skłamałem czy dotrzymałem słowa dopiero pojutrze 
W tym momencie mały Jaś (lat 5), synek Idioty nie wytrzymuje!
Jaś:
Tata, w moim przedszkolu uczą co następuje:
Definicja logiki matematycznej:
Logika to matematyczny opis nieznanego
… czyli nieznanej przyszłości lub nieznanej przeszłości (np. poszukiwanie mordercy)
Tata!
Dlaczego nie wiesz matematycznych banałów o których uczą w moim przedszkolu!
Prawo przejście ze zdaniem A do logiki przeciwnej:
Negujemy zmienne i wymieniamy spójniki na przeciwne
A: Y=K+T
stąd:
AU:
~Y=~K*~T
co matematycznie oznacza:
~Y=1 <=> ~K=1 i ~T=1
Czytamy:
Prawdą jest (=1) że skłamię (~Y) wtedy i tylko wtedy gdy jutro nie pójdziemy do kina (~K=1) i nie pójdziemy do teatru (~T=1)
Idiota:
Co za brednie ciebie uczą w tym twoim zasranym przedszkolu!
… jak skończysz studia matematyczne to zrozumiesz dlaczego twoja pani przedszkolanka bredzi!
Synek:
Tata, czy możesz powiedzieć jak wygląda logika matematyczna po studiach matematycznych?
Idiota:
Oczywiście, mogę mój kochany synku
Zdania prawdziwe w logice każdego matematyka to:
Jeśli świnie latają to krowy szczekają
Jeśli Prosiaczek jest wielbłądem to Kubuś jest misiem
Jeśli 2+2=5 to ty mój synku jesteś Papieżem
[link widoczny dla zalogowanych]
etc
Synek z płaczem:
Tata, jak to powiem w moim przedszkolu to wszyscy pękną ze śmiechu … ze mnie oczywiście.
|
|
| Powrót do góry |
|
 |
|
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Komandor
Gość
|
 Wysłany: Pon 12:46, 14 Mar 2016 Temat postu: Wysłany: Pon 12:46, 14 Mar 2016 Temat postu: |
|
|
Ładne kolorki 
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 16:02, 14 Mar 2016 Temat postu: Wysłany: Pon 16:02, 14 Mar 2016 Temat postu: |
|
|
| Komandor napisał: | Ładne kolorki  |
Zawsze twierdziłem Komandorze iż głupi nie jesteś - bo koniec końców musiałeś uznać genialność logiki matematycznej wszystkich 5-cio latków i humanistów 
Co innego Czarna Mańka - ta ma tak doszczętnie wyprany mózg, że nic już jej nie pomoże - musi tak zemrzeć biedaczka.
U Pana Baryckiego natomiast widzę światełko w ciemnym tunelu - ma szansę dołączyć do Ciebie.
Kubuś
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Adam Barycki
Gość
|
 Wysłany: Pon 16:35, 14 Mar 2016 Temat postu: Wysłany: Pon 16:35, 14 Mar 2016 Temat postu: |
|
|
Nie ma nawet Pan co myśleć o moim nawróceniu na AK, dopóki będą prostokąty, tylko złote jaja mogą mnie skusić do uczucia miłości do AK.
Adam Barycki
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 17:19, 14 Mar 2016 Temat postu: Wysłany: Pon 17:19, 14 Mar 2016 Temat postu: |
|
|
| Adam Barycki napisał: | Nie ma nawet Pan co myśleć o moim nawróceniu na AK, dopóki będą prostokąty, tylko złote jaja mogą mnie skusić do uczucia miłości do AK.
Adam Barycki |
Zupełnie Pana nie rozumiem Panie Barycki, zaparł się Pan jak osioł przed obliczem prawdy absolutnej - algebry Kubusia.
Czy chce Pan skończyć jak biedna Czarna Mańka?
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-375.html#272968
Stąd mamy prawo rozpoznawalności funkcji logicznej Y:
Funkcja logiczna Y jest rozpoznawalna wtedy i tylko wtedy gdy rozpoznawalna jest funkcja logiczna ~Y
Y<=>~Y=(Y=>~Y)*(~Y=>Y) =1*1 =1
Przykład
Załóżmy że znamy funkcję logiczną:
Y=p+q - funkcja logiczna w logice dodatniej (bo Y)
Prawo przejścia do logiki przeciwnej:
Negujemy zmienne i wymieniamy spójniki na przeciwne
~Y=~p*~q - funkcja logiczna w logice ujemnej (bo ~Y)
Oczywistym jest że jeśli nie znamy funkcji logicznej Y:
Y=?
to automatycznie nie znamy funkcji logicznej ~Y
~Y=~?
Prawo tożsamości wiedzy znane jest wszystkim 5-cio latkom, czego dowód w tym poście:
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-325.html#271334
Gdzie mali inżynierowie (oboje po 5 wiosenek) Zuzia i Jaś zaprojektowali najprawdziwsze sterowanie windą w logice dodatniej (bo Y) oraz niezależnie, w logice ujemnej (bo ~Y).
Dziwne jest że ziemscy matematycy, nie mają bladego pojęcia o tym zdecydowanie najważniejszym prawie matematycznym naszego Wszechświata.
Ile jeszcze wody w Wiśle musi upłynąć, aby wiedza matematyczna ziemskiego matematyka dorównała do wiedzy każdego 5-cio latka i humanisty?
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
hushek
Bloger na Kretowisku
Dołączył: 23 Lut 2011
Posty: 6781
Przeczytał: 0 tematów
Skąd: umiłowany kraj
Płeć: Mężczyzna
|
 Wysłany: Pon 20:48, 14 Mar 2016 Temat postu: Wysłany: Pon 20:48, 14 Mar 2016 Temat postu: |
|
|
Pszypominam umysłom ścisłym żesz jeich kurwa mać, tj. matematykom co jeich wena menczy, że dzisiaj (14.III.) obchodzimy Dzień

Wienc morze zamiast pierdolić czypoczy Kubusiowe abrakadabry może warto by jednak to jednak jakoś uczcić - matematyki niedokończone lup tesz niespełnione - kurna wasza mać - i na odwrut tj. skończone, rze nje powiem jusz co ...

|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pon 21:24, 14 Mar 2016 Temat postu: Wysłany: Pon 21:24, 14 Mar 2016 Temat postu: |
|
|
Hushek, blusa nie czujesz 
To już jest stypa po oficjalnym pogrzebie totalnie całej, ziemskiej logiki matematycznej ... a ty tu dupę zawracasz jakąś tam głupią literką Pi? 
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Adam Barycki
Gość
|
 Wysłany: Wto 7:19, 15 Mar 2016 Temat postu: Wysłany: Wto 7:19, 15 Mar 2016 Temat postu: |
|
|
Panie Kubusiu, jak Pan tak może niesprawiedliwie oceniać Pana Husheka, toż przecie Pan Hushek niczym innym nie posługuje się tak sprawnie, jak właśnie naturalnym prawem wszechświata, toż jest On najwierniejszym uczniem Pańskim, a że tego nie wie, to tylko dlatego, że takie właśnie jest naturalne prawo wszechświata, ameba też nie wie, a przecie Pan, Panie Kubusiu wie najlepiej, że co, jak co, ale ameba właśnie najsprawniej stosuje się do Algebry Kubusia, bo już u pięciolatków można zauważyć odchodzenie od naturalnego prawa wszechświata, jednak w procesie edukacji następuje powrót i po otrzymaniu dyplomu, taki magister współczesny, jako i ameba lub trzylatek jest całkowicie zintegrowanym z naturalnym prawem wszechświata. Przecie widzi Pan, Panie Kubusiu, że Pan Hushek równie sprawnie, jak i Pan, posługuje się Algebrą Kubusia. Pan wyciąga logiczny wniosek z oceny komunizmu, pisząc, że komuna była zła, bo zamiast szybko budować wieżowiec, wysyłała studentów w wakacje na Mazury, a Pan Hushek identycznie, jak Pan, dokonuje analizy komuny w absolutnej zgodzie z naturalnym prawem wszechświata, pisząc, że komuna była zła w Polsce, bo kapitalizm mógłby być lepszy, gdyby był lepszy, ale na razie jeszcze nie jest zupełnie lepszy, jednak lepszy zupełnie będzie niebawem, czego dowodem są co i rusz budowane szybko wieżowce, jak i malowane na ścianach strych kamienic murale, a także malowane elewacje starówek miejskich. Pani Agafia, też nie w kij dmuchał, mężnie dotrzymuje kroku pięciolatkom i pisze, że komunę dyskwalifikują wybudowane prze nią blokowiska. Komuna była zła, bo złe są blokowiska, a ponieważ blokowiska są złe, to komuna nie mogła być dobra. Tak więc, sam Pan widzi, Panie Kubusiu, że Algebra Kubusia zdobywa serca ludu i lud jej nie da zginąć.
Adam Barycki
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Janek
Gość
|
 Wysłany: Wto 10:42, 15 Mar 2016 Temat postu: Wysłany: Wto 10:42, 15 Mar 2016 Temat postu: |
|
|
| rafal3006 napisał: | Czytamy:
Prawdą jest (=1), że dotrzymam słowa (Y) wtedy i tylko wtedy gdy JUTRO pójdziemy do kina (K=1) lub pójdziemy do teatru (T=1)
Córcia:
Tata, kiedy zostaniesz (w przyszłości) kłamcą? |
Prawda jest taka, jaka wykładnia prawa.
Można tej prawdzie zadać kłam (złamać wykładnię prawa) i wtedy jest się Kłamcą, ale rozumieć to należy, że zadając kłam wykładni prawa musimy stworzyć kłam-stwo.
Kłamstwo jest ... praw-dziwe, o tyle że osoba zadająca kłam "prawi dziwy".
Przykład kłamcy to jest Kubuś, prawiący dziwy o krowach które latają. Uchowaj Boże... Cuda i Dziwy... Niech będzie pochwalony kłamca prawiący dziwy.
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
hushek
Bloger na Kretowisku
Dołączył: 23 Lut 2011
Posty: 6781
Przeczytał: 0 tematów
Skąd: umiłowany kraj
Płeć: Mężczyzna
|
 Wysłany: Wto 10:44, 15 Mar 2016 Temat postu: Wysłany: Wto 10:44, 15 Mar 2016 Temat postu: |
|
|
Oooo krowa dał - muuuu...,
Co to - przepustkę z Wariatkowa pan dochtur wypisał ? 
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
hushek
Bloger na Kretowisku
Dołączył: 23 Lut 2011
Posty: 6781
Przeczytał: 0 tematów
Skąd: umiłowany kraj
Płeć: Mężczyzna
|
 Wysłany: Wto 20:43, 15 Mar 2016 Temat postu: Wysłany: Wto 20:43, 15 Mar 2016 Temat postu: |
|
|
Zakaz sprzedaży wody w plastikowych butelkach
| Cytat: | Władze Montrealu podejmują walkę z plastikowymi śmieciami. Kanadyjskie miasto sprzeciwia się sprzedaży wody w butelkach wykonanych z tworzywa sztucznego.
W lutym tego roku burmistrz Montrealu wydał oświadczenie. Poinformował w nim, że zakaz sprzedaży jednorazowych toreb plastikowych wejdzie w życie w 2018 roku, a następne do odstrzału będą plastikowe butelki – podaje USA Today .
Poruszyłem sprawę plastikowych butelek, ponieważ są bardzo szkodliwe dla środowiska. Każdego roku ponad 700 milionów butelek jednorazowego użytku ląduje na wysypisku śmieci w Quebecu. W Montrealu mamy to szczęście, ze woda z kranu jest doskonałej jakości. Kilka razy dziennie poddawana jest testom sprawdzającym. Ludzie zapominają, że ta woda jest tak dobra i mogą mieć ją za darmo. Są firmy, które wlewają ją w plastikowe butelki i zarabiają na tym pieniądze. |

Pixabay.com
[link widoczny dla zalogowanych]
Bardzo mnie się podoba ta inicjatywa. Ale jest jeszcze cuś...
Rewolucja w ekologii? Odkryto bakterie, które żywią się plastikowymi butelkami
| Cytat: | Japońskim naukowcom udało się zidentyfikować bakterie, które żywią się plastikiem. Specjaliści zapewniają, że na tym etapie badania się nie skończyły. Być może bakterie wspomogą proces oczyszczania oceanów z plastikowych śmieci.
Grupa japońskich naukowców z Instytutu Technologicznego w Kioto znalazła gatunek bakterii, który żywi się... plastikiem. A dokładniej jednym jego rodzajem: tym, który wykorzystuje się do produkcji włókien sztucznych i butelek do napojów bezalkoholowych, czyli PET, jak skrótowo określa się poli(tereftalan etylenu), termoplastyczny polimer z grupy poliestrów.
Swoje odkrycie Japończycy opisali na łamach czwartkowego wydania magazynu "Science".
Odporny na biodegradację
Zaletą PET jest to, że jest on lekkim, bezbarwnym i wytrzymałym materiałem. Jest on również odporny na proces biodegradacji, co jednak należy dopisać do listy jego wad, ponieważ materiał ten dłużej się rozkłada. Wcześniejsze wyniki badań wykazały, że na PET może rosnąć kilka gatunków grzybów, jednak dopiero teraz odkryto jeden, który może dosłownie zjadać butelkę.
Aby znaleźć bakterię, która niszczy PET, zebrano 250 butelek z recyklingu. Miały one na sobie ślady piasku, wody, ścieków i innych zanieczyszczeń. Następnie przeanalizowano drobnoustroje, które na nich żyją. Naukowcy odkryli, że tylko jeden gatunek bakterii żywi się PET, dzięki czemu zyskuje on dodatkową energię i masę. Bakterie tę nazwano Ideonella sakainesis. Badania wykazały, że drobnoustroje te w zaledwie sześć tygodni przy stałej temperaturze równej 30 st. C mogłyby zdewastować cienką folię PET.
Specjaliści podają, że teraz będą analizować, czy przypadkiem nie istnieją jeszcze inne bakterie o takich samych właściwościach jak Ideonella sakainesis.
- Proces ten może być bardzo powszechny - twierdzi Tracy Mincer, autor badań. |
[link widoczny dla zalogowanych]
Jakaś nadzieja więc jest...dla natury. Gdyby tak jeszcze japońskim naukowcom udało sie wyhodować bakterie, które żarły by bez litości nijakiej szklane butelki bezzwrotne (zwrotne zaś zostawiały w spokoju) - o... to by było dopiero odkrycie 
Ostatnio zmieniony przez hushek dnia Wto 20:44, 15 Mar 2016, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Czw 20:49, 17 Mar 2016 Temat postu: Wysłany: Czw 20:49, 17 Mar 2016 Temat postu: |
|
|
Jak zwykle, z dedykacją dla Komandora, Czarnej Mańki i Pana Baryckiego
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-400.html#273596
Dowodzenie twierdzeń matematycznych
Wstęp teoretyczny:
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-375.html#271848
| rafal3006 napisał: | Algebra Kubusia
Nowa Teoria Zbiorów
Część I
1.0 Dekalog Nowej Teorii Zbiorów
1.
Symbole
„~” - symbol negacji (przeczenia), słówko „NIE” z naturalnego języka mówionego człowieka
„i”(*) - symbol iloczynu logicznego zbiorów p*q, spójnik „i”(*) w naturalnej logice człowieka
Y=p*q - wspólna część zbiorów p*q
„lub”(+) - symbol sumy logicznej zbiorów p+q, spójnik „lub”(+) w naturalnej logice człowieka
Y=p+q - wszystkie elementy zbiorów p i q bez powtórzeń
„-„ - różnica zbiorów p-q
Y=p-q - wszystkie elementy zbioru p pomniejszone o elementy zbioru q
Wartości logiczne:
1 = prawda
0 = fałsz
Definicja zbioru niepustego i pustego:
Zbiór jest niepusty gdy zawiera co najmniej jeden element
Zbiór jest pusty gdy nie zawiera żadnych elementów
Zbiory mają wartości logiczne:
p =[x] =1 - zbiór niepusty
p =[] =0 - zbiór pusty
Gdzie:
p - nazwa zbioru
[pies, kot …] - zawartość zbioru, wypisujemy elementy zbioru
p =[x] =1
Pierwsza tożsamość (=[x]) definiuje zbiór, natomiast druga (=1) przypisuje temu zbiorowi wartość logiczną
2.
Podstawowe definicje i działania na zbiorach
Definicja dziedziny:
Dziedzina to dowolny zbiór na którym operujemy, nic spoza dziedziny nas nie interesuje
Przyjmijmy dziedzinę:
D=[1,2,3,4,5,6] =1 - zbiór pełny
Definicja zaprzeczenia zbioru:
Zaprzeczenie zbioru to różnica dziedziny D i dowolnego zbioru x wewnątrz dziedziny (w tym D)
Oznaczmy:
D - dziedzina
Zaprzeczenie dziedziny to zbiór pusty []:
~D=[D-D] =[] =0 - zbiór pusty
Zaprzeczenie zbioru pustego to dziedzina:
~[] = D =1 - zbiór pełny (dziedzina)
Różnica zbiorów p-q:
Różnica zbiorów p-q to wszystkie elementy zbioru p pomniejszone o elementy zbioru q
Zdefiniujmy zbiory p i q:
p=[1,2,3,4] =1 - zbiór wejściowy niepusty
q=[3,4,5,6]
~p =[D-p] =[1,2,3,4,5,6]-[1,2,3,4] =[5,6] =1 - zbiór wynikowy niepusty
~q =[D-q] =[1,2,3,4,5,6]-[3,4,5,6] =[1,2]
Iloczyn logiczny zbiorów:
Iloczyn logiczny zbiorów p*q to wspólna część tych zbiorów
Y = p*q = [1,2,3,4]*[3,4,5,6] = [3,4] =1 - bo zbiór wynikowy niepusty
Suma logiczna zbiorów:
Suma logiczna zbiorów p+q to wszystkie elementy zbiorów p i q bez powtórzeń
Y=p+q = [1,2,3,4]+[3,4,5,6] = [1,2,3,4,5,6] =1 - bo zbiór wynikowy niepusty
3.
Podzbiór =>
Zbiór p jest podzbiorem zbioru q wtedy i tylko wtedy gdy każdy element zbioru p należy do zbioru q
p=>q - zbiór p jest podzbiorem => q
p=>q =1 - prawda (=1), gdy rzeczywiście p jest podzbiorem q (inaczej: fałsz =0)
Konsekwencje w zbiorach:
p=>q = [p*q =p]
4.
Nadzbiór ~>
Zbiór p jest nadzbiorem zbioru q gdy zawiera w sobie wszystkie elementy zbioru q
p~>q - zbiór p jest nadzbiorem ~> q
p~>q =1 - prawda (=1), gdy rzeczywiście p jest nadzbiorem ~> q (Inaczej: fałsz =0)
Konsekwencje w zbiorach:
p~>q = [p*q=q]
Przykład:
D=[1,2,3,4,5,6] - dziedzina
p=[1,2] - zbiór p
q=[1,2,3,4] - zbiór q
Podzbiór => vs nadzbiór ~>:
p=>q =1 - bo zbiór p jest podzbiorem => zbioru q
p~>q =0 - bo zbiór p nie jest nadzbiorem ~> zbioru q
Nadzbiór ~> vs podzbiór =>:
q~>p =1 - bo zbiór q jest nadzbiorem ~> zbioru p
q=>p =0 - bo zbiór q nie jest podzbiorem => zbioru p
5.
Zbiory tożsame
p=q
Zbiory p i q nazywamy tożsamymi wtedy i tylko wtedy, gdy każdy element zbioru p należy => do zbioru q i każdy element zbioru q należy => do zbioru p
Innymi słowy:
Zbiory p i q nazywamy tożsamymi wtedy i tylko wtedy, gdy każdy element zbioru p jest podzbiorem => zbioru q i każdy element zbioru q jest podzbiorem => zbioru p
p=q <=> (p=>q)*(q=>p)
Matematycznie zachodzi tożsamość:
należy => do zbioru p = jest podzbiorem => zbioru p
6.
Kwantyfikator mały p~~>q
Definicja kwantyfikatora małego w zbiorach:
\/x p(x)~~>q(x) = p(x)*q(x)
Istnieje takie x, które należy jednocześnie do zbiorów p(x) i q(x)
Kwantyfikator mały ~~> jest tożsamy z iloczynem logicznym zbiorów p*q
p~~>q = p*q =1 - prawda (=1), gdy zbiór p ma wspólny element ze zbiorem q (Inaczej: Fałsz =0)
Definicja kwantyfikatora małego ~~> w zdarzeniach:
Możliwe jest ~~> (=1) jednoczesne zajście zdarzeń p i q (inaczej =0)
Przykład:
P~~>CH =P*CH =1 - „Pada” i „są chmury” zdarzenie możliwe (=1)
P~~>~CH =P*~CH =0 - „Pada” i „nie ma chmur” - zdarzenie niemożliwe (=0)
7.
Warunek wystarczający =>
Definicja warunku wystarczającego => w zbiorach:
p=>q - zbiór p jest podzbiorem => zbioru q
p=[1,2]
q=[1,2,3,4]
Mówimy że p jest wystarczające => dla q wtedy i tylko wtedy gdy każdy element zbioru p należy do zbioru q.
Wylosowanie dowolnej liczby ze zbioru p jest warunkiem wystarczającym => do tego, aby ta liczba należała do zbioru q
Wylosowanie dowolnej liczby ze zbioru p daje nam gwarancję matematyczną => przynależności tej liczby do zbioru q
Wymuszam dowolne p i musi => pojawić się q.
Warunek wystarczający => dotyczy zarówno dowolnych elementów zbiorów p i q jak i kompletnych zbiorów.
Wymuszam kompletny zbiór p i mam gwarancję matematyczną, że ten zbiór jest podzbiorem => zbioru q
Matematycznie zachodzi:
Warunek wystarczający => = Gwarancja matematyczna => = podzbiór => p w obrębie zbioru q
Definicja kwantyfikatora dużego w zbiorach:
/\x p(x) => q(x)
Dla każdego elementu x, jeśli element x należy do zbiory p(x) to mamy gwarancję matematyczną => iż element x należy do zbioru q(x)
Definicja warunku wystarczającego => w zdarzeniach:
p=>q - zajście zdarzenia p jest warunkiem wystarczającym => dla zajścia zdarzenia q
Przykład:
P=>CH - zdarzenie „pada” jest warunkiem wystarczającym => dla istnienia „chmur”
8.
Warunek konieczny ~>
Definicja warunku koniecznego ~> w zbiorach:
p~>q - zbiór p jest nadzbiorem ~> dla zbioru q
p=[1,2,3,4]
q=[1,2]
Mówimy że p jest konieczne ~> dla q wtedy i tylko wtedy gdy zbiór p zawiera w sobie wszystkie elementy zbioru q
Zabieram wszystkie elementy zbioru p i znika mi zbiór q
Zabieram kompletny zbiór p i znika mi zbiór q
Zauważmy, że warunek konieczny ~> to fundamentalnie co innego niż warunek wystarczający =>.
Dowód:
Jeśli wylosuję dowolny element zbioru p to nie mam żadnej gwarancji matematycznej => iż ten element będzie należał do zbioru q
Przykład: liczba 3 należy do zbioru p i nie należy do zbioru q.
Definicja warunku koniecznego ~> w zdarzeniach:
p~>q - zajście zdarzenia p jest konieczne ~> dla zaistnienia zdarzenia q
Przykład:
CH~>P - istnienie „chmur” jest konieczne ~> do tego, by „padało”
Zabieram chmury wykluczając możliwość padania.
9.
Zdanie warunkowe „Jeśli p to q”
Definicja zdania warunkowego „Jeśli p to q”
Jeśli p to q
gdzie:
p - poprzednik
q - następnik
Zdanie warunkowe „Jeśli p to q” w zbiorach opisuje wzajemną relację zbiorów p i q
Zdanie warunkowe „Jeśli p to q” w zdarzeniach opisuje wzajemną relację zdarzeń p i q
Definicja warunku wystarczającego => w zbiorach:
A.
Jeśli zajdzie p to na pewno => zajdzie q
p=>q
Warunek wystarczający p=>q =1 jest spełniony (=1) wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q (Inaczej: p=>q =0)
Warunek wystarczający można zapisać w sposób tożsamy przy pomocy kwantyfikatora dużego:
/\x p(x)=>q(x)
Dla każdego elementu x, jeśli element x należy do zbioru p(x) to mamy gwarancję matematyczną => iż ten sam element należy do zbioru q(x)
Przykład:
Jeśli liczba jest podzielna przez 8 to na pewno => jest podzielna przez 2
P8=>P2 =1
Definicja warunku wystarczającego => spełniona bo zbiór P8=[8,16,24..] jest podzbiorem => zbioru P2=[2,4,6,8..]
Definicja warunku wystarczającego => w zdarzeniach:
A.
Jeśli zajdzie p to na pewno => zajdzie q
p=>q
Warunek wystarczający => jest spełniony wtedy i tylko wtedy gdy zajście zdarzenia p wymusza zajście zdarzenia q.
Przykład:
Jeśli jutro będzie padało to na pewno => będzie pochmurno
P=>CH =1
Padanie deszczu jest warunkiem wystarczającym => dla istnienia chmur
Definicja warunku koniecznego ~> w zbiorach:
A.
Jeśli zajdzie p to może ~> zajść q
p~>q
Warunek konieczny p~>q =1 jest spełniony (=1) wtedy i tylko wtedy gdy zbiór p jest nadzbiorem ~> zbioru q (Inaczej: p~>q =0)
Przykład:
Jeśli liczba jest podzielna przez 2 to może ~> być podzielna przez 8
P2~>P8 =1
Definicja warunku koniecznego spełniona bo zbiór P2=[2,4,6,8..] jest nadzbiorem ~> zbioru P8=[8,16,24..]
Definicja warunku koniecznego ~> w zdarzeniach:
A.
Jeśli jutro będzie pochmurno to może ~> padać
CH~>P =1
Definicja warunku koniecznego ~> spełniona bo zabieram chmury wykluczając padanie.
Definicja kwantyfikatora małego ~~>
A.
Jeśli zajdzie p to może ~~> zajść q
p~~>q = p*q
Kwantyfikator mały p~~>q =1 jest spełniony (=1) gdy istnieje wspólny element zbiorów p*q (Inaczej: p~~>q =0)
Zapis tożsamy:
\/x p(x)~~>q(x) = p(x)*q(x)
Istnieje takie x, które należy jednocześnie do zbiorów p(x) i q(x)
Przykład:
Zbiory:
Jeśli liczba jest podzielna przez 8 to może ~~> być podzielna przez 2
P8~~>P2 =P8*P2 =1 bo 8 - istnieje wspólny element zbiorów P8=[8,16,24..] i P2=[2,4,6,8 ..]
Zdarzenia:
Jeśli jutro będzie padało to może ~~> być pochmurno
P~~>CH = P*CH =1 - możliwa jest (=1) sytuacja „pada” i „są chmury”
10.
Definicja kontrprzykładu w zbiorach
Definicja warunku wystarczającego => w zbiorach:
A.
Jeśli zajdzie p to na pewno => zajdzie q
p=>q
Warunek wystarczający p=>q =1 jest spełniony (=1) wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q (Inaczej: p=>q =0)
Prawdziwość warunku wystarczającego A gwarantuje fałszywość kontrprzykładu B (i odwrotnie)
B.
Jeśli zajdzie p to może ~~> zajść ~q
p~~>~q = p*~q
Kwantyfikator mały p~~>~q =1 jest spełniony (=1) gdy istnieje wspólny element zbiorów p*~q (Inaczej: p~~>~q =0)
Definicja kontrprzykładu w zbiorach:
Kontrprzykładem dla warunku wystarczającego p=>q nazywamy to samo zdanie z zanegowanym następnikiem kodowane kwantyfikatorem małym p~~>~q =p*~q
Rozstrzygnięcia:
10-1.
Prawdziwość kontrprzykładu p~~>~q =p*~q =1 daje nam gwarancję matematyczną fałszywości zdania kodowanego warunkiem wystarczającym p=>q =0 (i odwrotnie)
10-2.
Fałszywość kontrprzykładu p~~>~q =p*~q =0 daje nam gwarancję matematyczną prawdziwości warunku wystarczającego p=>q=1 (i odwrotnie) |
| fiklit napisał: | | Ale dlaczego p=>q=1 piszesz w lini A. Skoro to jest wniosek z jedynki w linii A i zera w linii B? |
Dzięki, o takie posty mi chodzi.
| Kod: |
Tabela 1
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach „lub”(+) i „i”(*) |w spójnikach „lub”(+) i „i”(*)
Y1=p<=>q=p*q+~p*~q | Y2=p|=>q=p*q+~p*~q+~p*q
A1: p* q =1 |A2: p* q =1
B1: p*~q =0 |B2: p*~q =0
C1:~p*~q =1 |C2:~p*~q =1
D1:~p* q =0 |D2:~p* q =1
|
| Kod: |
Tabela 2
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach =>, ~> i ~~> |w spójnikach =>, ~> i ~~>
Y3=p<=>q=(p=>q)*[p=q] | Y4=p|=>q=(p=>q)*~[p=q]
A3: p=> q =[ p* q= p] =1 |A4: p=> q =[ p* q= p] =1
B3: p~~>~q= p*~q =0 |B4: p~~>~q= p*~q =0
C3:~p=>~q =[~p*~q=~q] =1 |C4:~p~>~q =[~p*~q=~q] =1
D3:~p~~>q = ~p* q =0 |D4:~p~~>q = ~p* q =1
|
Zakładam, że rozumiesz i akceptujesz tabele symboliczne w spójnikach „lub”(+) i „i”(*):
A1-D1 i A2-D2
W rzeczywistości:
Jeśli dowolnej serii zdań A, B, C i D możemy przyporządkować jedną z powyższych tabel, to matematycznie nie mamy nic do roboty, wszystko mamy udowodnione w 100% i nic więcej z tego nie wyciśniemy.
| rafal3006 napisał: |
10.
Definicja kontrprzykładu w zbiorach:
Kontrprzykładem dla warunku wystarczającego p=>q nazywamy to samo zdanie z zanegowanym następnikiem kodowane kwantyfikatorem małym p~~>~q =p*~q
Rozstrzygnięcia:
10-1.
Prawdziwość kontrprzykładu p~~>~q =p*~q =1 daje nam gwarancję matematyczną fałszywości zdania kodowanego warunkiem wystarczającym p=>q =0 (i odwrotnie)
10-2.
Fałszywość kontrprzykładu p~~>~q =p*~q =0 daje nam gwarancję matematyczną prawdziwości warunku wystarczającego p=>q=1 (i odwrotnie) |
W rzeczywistości nieznanej (nieznanej przyszłości) mamy jedną wielką niewiadomą czyli nasza tabela wejściowa A1-D1 wygląda tak:
| Kod: |
A1: p* q =?
B1: p*~q =?
C1:~p*~q =?
D1:~p* q =?
|
Załóżmy, że udało się nam udowodnić iż w linii B1 zachodzi:
B1: p*~q =0 - zbiory rozłączne
Jakie są tego faktu konsekwencje?
Na mocy najważniejszego przykazania 10-2 z dekalogu Nowej Teorii Zbiorów konsekwencje tego faktu są WIELKIE!
| Kod: |
Tabela 1
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach „lub”(+) i „i”(*) |w spójnikach „lub”(+) i „i”(*)
Y1=p<=>q=p*q+~p*~q =? | Y2=p|=>q=p*q+~p*~q+~p*q=?
A1: p* q =1 |A2: p* q =1
B1: p*~q =0 |B2: p*~q =0
C1:~p*~q =1 |C2:~p*~q =1
D1:~p* q =? |D2:~p* q =?
|
| Kod: |
Tabela 2
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach =>, ~> i ~~> |w spójnikach =>, ~> i ~~>
Y3=p<=>q=(p=>q)*[p=q]=?| Y4=p|=>q=(p=>q)*~[p=q]=?
A3: p=> q =[ p* q= p] =1 |A4: p=> q =[ p* q= p] =1
B3: p~~>~q= p*~q =0 |B4: p~~>~q= p*~q =0
C3:~p~>~q =[~p*~q=~q] =1 |C4:~p~>~q =[~p*~q=~q] =1
D3:~p~~>q = ~p* q =? |D4:~p~~>q = ~p* q =?
|
Jak widzimy, po udowodnieniu iż:
A1: p*~q=0 - zbiory rozłączne
Wiemy prawie wszystko, z wyjątkiem wisienki na torcie, linii Dx=?
Skąd się to wzięło?
Wynikowe 0 w linii B1 transmituje się do linii B2, B3 i B4.
Wynikowe 0 w linii B1=B2=B3=B4 na mocy świętego przykazania 10-2 wymusza warunek wystarczający p=>q w liniach A3 i A4.
Warunki wystarczające => w liniach A3 i A4 wymuszają warunki konieczne ~> w liniach C3 i C4.
W sprzężeniu zwrotnym wymusza to wynikowe jedynki w liniach C1 i C2
Zauważmy, że w tym momencie wiemy bardzo dużo ale nie potrafmy jeszcze zapisać funkcji logicznych Y1, Y2, Y3 i Y4 bo nie wiemy co się dzieje w linii Dx=?
UWAGA!
Zauważmy, że zachodzi też odwrotnie, czyli dokładnie ten sam stan tablic uzyskamy udowadniając prawdziwość zdania:
A3: p=>q =[p*q=p] =1
Definicja warunku wystarczającego p=>q:
Jeśli zajdzie p to na pewno => zajdzie q
p=>q [p*q=p] =1
Definicja warunku wystarczającego spełniona wtedy i tylko wtedy gdy zbiór p jest podzbiorem => zbioru q
Wylosowanie dowolnego elementu ze zbioru p jest warunkiem wystarczającym => na to, by ten element należał do zbioru q
Wylosowanie dowolnego elementu ze zbioru p daje nam gwarancję matematyczną => iż ten element będzie należał do zbioru q
Matematycznie zachodzi:
Warunek wystarczający => = Gwarancja matematyczna =>
Konsekwencje dowodu:
A3: p=>q = [p*q=p] =1
Warunek wystarczający A3 wymusza w linii B3 wynikowe zero na mocy świętego przykazania 10-2 oraz warunek konieczny ~> w linii C3.
Mamy zatem:
B3: p~~>~q = p*~q =0
C3: ~p~>~q = [~p*~q=~q] =1
Oczywistym jest, że wynikowe zera i jedynki z linii A3, B3 i C3 przenoszą się na wszystkie pozostałe tabele do odpowiednich linii.
A3=A4=A1=A2
B3=B4=A1=A2
C3=C4=C1=C2
| rafal3006 napisał: |
10.
Definicja kontrprzykładu w zbiorach:
Kontrprzykładem dla warunku wystarczającego p=>q nazywamy to samo zdanie z zanegowanym następnikiem kodowane kwantyfikatorem małym p~~>~q =p*~q
Rozstrzygnięcia:
10-1.
Prawdziwość kontrprzykładu p~~>~q =p*~q =1 daje nam gwarancję matematyczną fałszywości zdania kodowanego warunkiem wystarczającym p=>q =0 (i odwrotnie)
10-2.
Fałszywość kontrprzykładu p~~>~q =p*~q =0 daje nam gwarancję matematyczną prawdziwości warunku wystarczającego p=>q=1 (i odwrotnie) |
W przykazaniu 10=2 końcowe słówko „i odwrotnie” oznacza że:
10-2’:
Prawdziwość warunku wystarczającego p=>q =1 daje nam gwarancję matematyczną fałszywości kontrprzykładu p~~>~q =0.
Dokładnie z tego faktu skorzystaliśmy w rozważaniach odwrotnych wyżej.
Kiedy możemy jednoznacznie rozstrzygnąć z jakim diabłem mamy do czynienia, czyli kiedy możemy zapisać jednoznacznie funkcje logiczne Y1, Y2, Y3 i Y4?
Oczywiście wtedy i tylko wtedy gdy rozstrzygniemy co się dzieje w linii Dx=?
I.
Załóżmy ze udowodnimy iż:
Dx=~p*q =1 - zbiory ~p i q mają część wspólną
Wtedy nasze tabele przyjmą postać:
| Kod: |
Tabela 1
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach „lub”(+) i „i”(*) |w spójnikach „lub”(+) i „i”(*)
Y1=p<=>q=p*q+~p*~q =0 | Y2=p|=>q=p*q+~p*~q+~p*q=1
A1: p* q =1 |A2: p* q =1
B1: p*~q =0 |B2: p*~q =0
C1:~p*~q =1 |C2:~p*~q =1
D1:~p* q =1 |D2:~p* q =1
|
| Kod: |
Tabela 2
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach =>, ~> i ~~> |w spójnikach =>, ~> i ~~>
Y3=p<=>q=(p=>q)*[p=q]=0| Y4=p|=>q=(p=>q)*~[p=q]=1
A3: p=> q =[ p* q= p] =1 |A4: p=> q =[ p* q= p] =1
B3: p~~>~q= p*~q =0 |B4: p~~>~q= p*~q =0
C3:~p~>~q =[~p*~q=~q] =1 |C4:~p~>~q =[~p*~q=~q] =1
D3:~p~~>q = ~p* q =1 |D4:~p~~>q = ~p* q =1
|
Doskonale widać, że w tym przypadku mamy do czynienia z implikacją prostą p|=>q prawdziwą opisaną tabelami A2-D2 i A4-D4.
Zauważmy że:
Jeśli cokolwiek jest implikacją prostą p|=>q =1 to nie ma prawa być równoważnością p<=>q =0.
W tym przypadku warunek wystarczający p=>q wchodzi w skład definicji symbolicznej implikacji prostej p|=>q.
Twierdzenia matematyczne to wyłącznie warunki wystarczające p=>q.
Mówienie że warunek wystarczający p=>q to jest to samo co implikacja prosta p|=>q jest błędem czysto matematycznym powszechnym w logice matematycznej ziemian.
Najwyższy czas z tym skończyć!
Implikacja prosta p|=>q to seria czterech zdań A4,B4,C4 i D4 a nie jedno zdanie z definicji symbolicznej. W szczególności na pewno implikacją prostą p|=>q nie jest warunek wystarczający p=>q (twierdzenie matematyczne) wchodzący w skład definicji implikacji prostej p|=>q.
II.
Załóżmy ze udowodnimy iż:
Dx=~p*q =0 - zbiory ~p i q są rozłączne
Nasze ostateczne tabele prawdy przyjmują w tym przypadku postać:
| Kod: |
Tabela 1
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach „lub”(+) i „i”(*) |w spójnikach „lub”(+) i „i”(*)
Y1=p<=>q=p*q+~p*~q =1 | Y2=p|=>q=p*q+~p*~q+~p*q=0
A1: p* q =1 |A2: p* q =1
B1: p*~q =0 |B2: p*~q =0
C1:~p*~q =1 |C2:~p*~q =1
D1:~p* q =0 |D2:~p* q =0
|
| Kod: |
Tabela 2
Definicja równoważności p<=>q |Definicja implikacji prostej p|=>q
w spójnikach =>, ~> i ~~> |w spójnikach =>, ~> i ~~>
Y3=p<=>q=(p=>q)*[p=q]=1| Y4=p|=>q=(p=>q)*~[p=q]=0
A3: p=> q =[ p* q= p] =1 |A4: p=> q =[ p* q= p] =1
B3: p~~>~q= p*~q =0 |B4: p~~>~q= p*~q =0
C3:~p~>~q =[~p*~q=~q] =1 |C4:~p~>~q =[~p*~q=~q] =1
D3:~p~~>q = ~p* q =0 |D4:~p~~>q = ~p* q =0
|
Doskonale widać, że w tym przypadku mamy do czynienia z równoważnością prawdziwą p<=>q=1 opisaną tabelami A1-D1 i A3-D3.
Zauważmy, że w równoważności p<=>q na mocy definicji mamy do czynienia z tożsamością zbiorów p=q wymuszającą tożsamość zbiorów ~p=~q.
Dokładnie z tego powodu w linii D3 wymuszone zostaje 0.
Z powodu tożsamości zbiorów ~p=~q w linii C3 spełniony jest jednocześnie warunek konieczny ~p~>~q (to stwierdziliśmy udowadniając p=>q=1) oraz warunek wystarczający ~p=>~q (to stwierdzamy w tym momencie na mocy świętego przykazania 10-2)
W ten sposób otrzymujemy jedną z możliwych definicji równoważności:
~p<=>~q = (~p~>~q)*(~p=>~q)
Równoważność to jednoczesne zachodzenie warunku koniecznego ~> i wystarczającego => między tymi samymi punktami.
Powyższa równoważność określa nam co się dzieje po stronie zbiorów ~p=~q.
Przykład:
Trójkąt nie jest prostokątny wtedy i tylko wtedy gdy nie zachodzi suma kwadratów
~TP<=>~SK
Po stronie zbiorów p=q równoważność będzie następująca:
p<=>q = (p~>q)*(p=>q)
Przykład:
Trójkąt jest prostokątny wtedy i tylko wtedy gdy zachodzi suma kwadratów
TP<=>SK
Uwaga!
W ostatnim kroku udowodniliśmy równoważność dowodząc rozłączności zbiorów w linii D3:
D3: ~p~~>q = ~p*q =0 - zbiory rozłączne.
Dowód alternatywny!
W równoważności na mocy definicji w linii D3 musi być 0 - zbiory rozłączne.
Znów korzystamy z najwyższej świętości matematycznej - przykazania 10-2.
| rafal3006 napisał: |
10.
Definicja kontrprzykładu w zbiorach:
Kontrprzykładem dla warunku wystarczającego p=>q nazywamy to samo zdanie z zanegowanym następnikiem kodowane kwantyfikatorem małym p~~>~q =p*~q
Rozstrzygnięcia:
10-1.
Prawdziwość kontrprzykładu p~~>~q =p*~q =1 daje nam gwarancję matematyczną fałszywości zdania kodowanego warunkiem wystarczającym p=>q =0 (i odwrotnie)
10-2.
Fałszywość kontrprzykładu p~~>~q =p*~q =0 daje nam gwarancję matematyczną prawdziwości warunku wystarczającego p=>q=1 (i odwrotnie) |
Na mocy przykazania 10-2 alternatywny dowód iż w punkcie D3 mamy 0 to wykazanie prawdziwości warunku wystarczającego:
C3: ~p=>~q =1
Definicja warunku wystarczającego => spełniona wtedy i tylko wtedy gdy zbiór ~p jest podzbiorem => zbioru ~q.
Tożsama definicja równoważności:
p<=>q = (p=>q)*(~p=>~q)
Twierdzenie C3: ~p=>~q nosi nazwę twierdzenia odwrotnego do A3: p=>q
W równoważności (i tylko tu!) zachodzi prawo kontrapozycji:
~p=>~q = q=>p
Stąd mamy tożsamą definicję równoważności uwielbianą przez matematyków:
p<=>q = (p=>q)*(q=>p)
Stąd zamiast dowodzić iż zbiór ~p jest podzbiorem ~q (~p=>~q) w twierdzeniu odwrotnym C3 możemy dowodzić iż zbiór q jest podzbiorem => zbioru p (q=>p).
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
hushek
Bloger na Kretowisku
Dołączył: 23 Lut 2011
Posty: 6781
Przeczytał: 0 tematów
Skąd: umiłowany kraj
Płeć: Mężczyzna
|
 Wysłany: Sob 7:08, 19 Mar 2016 Temat postu: Wysłany: Sob 7:08, 19 Mar 2016 Temat postu: |
|
|
Polscy naukowcy odkryli prehistoryczne naczynia krwionośne
| Cytat: | Polscy naukowcy odkryli prehistoryczne naczynia krwionośne w kościach dinozaurów liczących prawie ćwierć miliarda lat. To pierwsze tego typu odkrycie na świecie. – Współczesne wykopaliska będą wykonywane w materiale genetycznym, a nie w plenerze. Tam jest zapisana cała prawda o naszej historii – mówił dr Andrzej Boczarowski podczas prezentacji odkrycia na Uniwersytecie Śląskim w Katowicach.
Opisanego przez polskich naukowców na łamach prestiżowego magazynu naukowego PLOS One odkrycia dokonano w kościach gadów ziemnowodnych i lądowych - notozaura i tanystrofa. Szczątki zwierząt zostały znalezione w Gogolinie na Opolszczyźnie, oraz w dzielnicy Miasteczka Śląskiego – Żyglinie, niedaleko Tarnowskich Gór. Skamieniałe naczynia krwionośne z zachowanymi chemicznymi śladami białek w kościach, zachowały się dzięki szybkiej mineralizacji, co musiało nastąpić gwałtownie, by umożliwić zachowanie się tych struktur. Naukowcy przypuszczają, że po zgonie gadów ich ciała zostały błyskawicznie pochowane, co hamując rozkład, ocaliło szczątki.
|
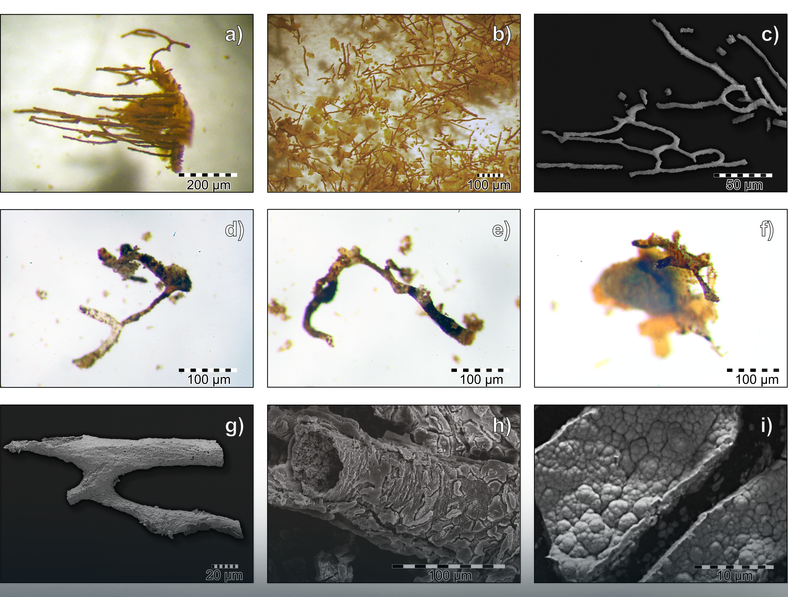
Foto: Materiały prasowe
| Cytat: | Okazuje się, że w ścianach naczyń krwionośnych pochodzących z ciał gadów triasowych, odkrytych na Śląsku zachował się także kolagen, ale trzykrotnie starszy od opisywanego przez prof. Pawlickiego, co zostało potwierdzone badaniami, przy których pracował zespół naukowców. Badania prowadzili paleontolodzy: mgr Dawid Surmik, dr Andrzej Boczarowski oraz fizycy ciała stałego: prof. Jacek Szade, dr Katarzyna Balin, fizyk molekularny dr Mateusz Dulski, biogeolog dr hab. Barbara Kremer oraz histolog i morfolog prof. Roman Pawlicki.
Badanie materiału prowadzone były kilkoma uzupełniającymi się metodami, przy użyciu najnowocześniejszego sprzętu ze Śląskiego Centrum Edukacji i Badań Interdyscyplinarnych w Chorzowie. Jak wskazują naukowcy, było to pierwsze w Polsce wykorzystanie takich urządzeń w badaniach próbek kopalnych. Użyto analiz z środowiskowego mikroskopu skaningowego (ESEM), spektroskopii w podczerwieni (FTIR) oraz rentgenowskiej spektroskopii fotoelektronowej (XPS). Wykorzystano także wysokorozdzielczy spektrometr mas jonów wtórnych z analizą czasu przelotu (ToF-SIMS), którzy umożliwia bardzo precyzyjne określenie składu chemicznego analizowanych próbek. |
[link widoczny dla zalogowanych]
No proszę - tera wystarczy sklonować gadziory i teoria starego Giertycha o współżyciu zgodnym smoków i ludzi bedzie miała swoje naukowe potwierdzenie. I skonczą się wreszcie darwinowskie protesty w szkołach, że ksionszki pan prof. pisze take nieco nie halo.
Nawet składa sjem to fszystko do kupy - pan redachtor był uprzejmy napisać bowiem, że dino zostały niezwłocznie pochowane
No wienc kto je pochował ? Chyba no nie kuzynowstwo-dinozaurostwo - ani chybi ludzie jakieś wierzonce. Co prawda w datach to się jakoś nie składa, ale to pewno pomyłka tech naukowców - miało być 2500 lat,a jebli siem o pare zer i wyjszło Jiem 2 500 000 
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pią 11:40, 01 Kwi 2016 Temat postu: Wysłany: Pią 11:40, 01 Kwi 2016 Temat postu: |
|
|
Smutny koniec logiki matematycznej twardogłowych: Komandora i Czarnej Mańki 
http://www.sfinia.fora.pl/forum-kubusia,60/prawo-subalternacji,8368-500.html
Dowód wewnętrznej sprzeczności logiki matematycznej ziemian!
Rozważmy zdanie pani przedszkolanki:
A.
Jutro pójdziemy do kina lub do teatru
Y=K+T
| Kod: | Tabela prawdy dla zdania Y=K+T
K T Y=K+T
A: 1 1 =1
B: 1 0 =1
C: 0 1 =1
D: 0 0 =0 |
Równanie prof. Newelskiego, czyli spis z natury (piszę to co widzę) w naturalnej logice matematycznej człowieka:
1.
1ABC: Y=1 <=> A: K=1 i T=1 lub B: K=1 i T=0 lub K=0 i T=1
Jedynki i zera w równaniu prof. Newelskiego nie mogą być prawdą i fałszem bezwzględnym, bo wtedy logika ziemian jest wewnętrznie sprzeczna.
Dowód:
A: T=1 i B: T=0
cnd
Jedynki i zera w równaniu prof. Newelskiego opisują nieznaną przyszłość!
Czyli opisują trzy, niezależne i rozłączne sytuacje w przyszłości:
A: K=1 i T=1 - jutro pójdę do kina (K=1) i do teatru (T=1)
lub
B: K=1 i T=0 - jutro pójdę do kina (K=1) i nie pójdę do teatru (T=0)
lub
C: K=0 i T=1 - jutro nie pójdę do kina (K=0) i pójdę do teatru (T=1)
Wniosek:
Poprawne znaczenie jedynek i zer w równaniu prof. Newelskiego może być tylko jedno.
To są prawdy i fałsze względne które w przyszłości mogą zaistnieć, ale nie muszą.
Dopiero w świecie zdeterminowanym, czyli pojutrze, gdy znamy rozwiązanie, znamy wartości logiczne zmiennych binarnych w sensie bezwzględnym.
Załóżmy że wczoraj zaszło:
B.
K=1 i T=0 - wczoraj byliśmy w kinie (K=1) i nie byliśmy w teatrze (T=0)
Dopiero w tym przypadku znamy wartości bezwzględne (absolutne) zmiennych K i T.
Oczywiście w tym momencie symbole K i T przestają być zmiennymi binarnymi, stają się stałymi symbolicznymi o znanej wartości logicznej, której to wartości logicznej nie jesteśmy w stanie zmienić - czasu nie da się cofnąć!
Podsumowując:
Bez wprowadzenia do logiki matematycznej ziemian nowych pojęć:
prawda względna
fałsz względny
o znaczeniu jak wyżej, logika matematyczna ziemian jest wewnętrznie sprzeczna
cnd
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Czarna_Mańka
Dołączył: 31 Paź 2014
Posty: 2534
Przeczytał: 0 tematów
Płeć: Kobieta
|
 Wysłany: Pią 12:18, 01 Kwi 2016 Temat postu: Wysłany: Pią 12:18, 01 Kwi 2016 Temat postu: |
|
|
| rafal3006 napisał: | Smutny koniec logiki matematycznej twardogłowych: Komandora i Czarnej Mańki 
|
jeśli się łudzisz, że ja czytam te brednie - to porzuć złudzenia
a Komandora całuj po rękach - on jeden czyta - od czasu do czasu - te Twoje wydaliny,
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Komandor
Gość
|
 Wysłany: Pią 14:47, 01 Kwi 2016 Temat postu: Wysłany: Pią 14:47, 01 Kwi 2016 Temat postu: |
|
|
Coraz Rzadziej Maniu, coraz rzadziej... ale niech całuje...?
| Hushek napisał: | | ... o współżyciu zgodnym smoków i ludzi bedzie miała swoje naukowe potwierdzenie. |
Ale tan Maniek gupi.
Filmu "Jak wytresować smoka" nie oglądał czy co?
Ja na własne oczy widziałem jak ludzie w zgodzie ze smokami współżyli. Dokładnie Wikingowie.
Gupi ten Maniek i na dodatek nie obyty ani kulturalnie ani naukowo...
A pochowanie smoków? No cóż... jak współżyli to pewnie chowali.
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Gość
|
 Wysłany: Pią 15:07, 01 Kwi 2016 Temat postu: Wysłany: Pią 15:07, 01 Kwi 2016 Temat postu: |
|
|
| rafal3006 napisał: | Rozważmy zdanie pani przedszkolanki:
A.
Jutro pójdziemy do kina lub do teatru
Y=K+T |
Nawet dla takich jak Ja, pogoda nie jest do przewidzenia. Na przykład wczoraj miałem zamiar dzisiaj podbijać cegły. Ale nie da się, bo nie będę klęczał w błocie i za zimno jest.
Jutro może pójdę do sklepu po mleko i dlatego dzisiaj chyba się wymyję.
O, gdyby znalazła się ni stad ni z owąd jakaś chętna dziewczyna, może jutro wybrałbym się z nią do kina albo teatru...
A właściwie na chuj mi teatr lub kino z jakąś dziewczyną?
Jutro mogę zalutować Kingę jak się pokaże. Ale czy ona lubi lutowanie?
Chyba za gruba jest. jakaś taka przysadzista. Już wiem! Niech ona se kupi popcorn i idzie do kina z przedszkolanką. Niech ją łapie za kolanko. Przedszkolanki są do grzyba niepodobne, dzisiaj.
A jutro chuj im w dupe.
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pią 15:26, 01 Kwi 2016 Temat postu: Wysłany: Pią 15:26, 01 Kwi 2016 Temat postu: |
|
|
| Czarna_Mańka napisał: | | rafal3006 napisał: | Smutny koniec logiki matematycznej twardogłowych: Komandora i Czarnej Mańki 
|
jeśli się łudzisz, że ja czytam te brednie - to porzuć złudzenia
a Komandora całuj po rękach - on jeden czyta - od czasu do czasu - te Twoje wydaliny,
|
Kurde, Komandorze, z kim ty się zdajesz?
Czarna Mańka ma pancerny kaganiec na mózgu - proponuję ją konsekwentnie ignorować, bo do tej baby żadna nowa wiedza nigdy nie dotrze.
Z dedykacją dla Komandora i Pana Baryckiego, mających na głowach mózgi zdolne pojąć o co chodzi w logice matematycznej 5-cio latków i humanistów - wierzę w was Panowie 
http://www.sfinia.fora.pl/forum-kubusia,12/prawo-subalternacji,8368-500.html#275230
| fiklit napisał: | | Wydumane to strasznie. |
Pozwolisz że na początek zacznę rzeczowo i absolutnie bez żadnego wydumania, po prostu zacytuję prof. Newelskiego.
Pani w przedszkolu do 5-cio latków:
A.
Jutro pójdziemy do kina lub do teatru
Y=K+T
Zbudujmy tabelę prawdy dla tego zdania:
| Kod: |
Tabela prawdy dla zdania Y=K+T
K T Y=K+T
A: 1 1 =1
B: 1 0 =1
C: 0 1 =1
D: 0 0 =0
|
Równanie algebry Boole’a (sic!) prof. Newelskiego, czyli spis z natury (piszę to co widzę) w naturalnej logice matematycznej człowieka:
1.
1ABC: Y=1 <=> A: K=1 i T=1 lub B: K=1 i T=0 lub K=0 i T=1
Czy możesz odpowiedzieć na proste pytania?
1.
Czym są symbole K, T oraz Y w nagłówku powyższej tabeli?
Możliwości masz wyłącznie dwie:
A.
To są zmienne binarne których wartości logicznej w dniu dzisiejszym (w chwili wypowiadania zdania Y=K+T) nie znamy
B.
To są stałe symboliczne których wartość logiczna jest znana i której to wartości logicznej nie jesteśmy w stanie zmienić
2.
Czym są zera i jedynki w równaniu algebry Boole’a (sic!) prof. Newelskiego?
A.
W szczególności czy te jedynki i zera oznaczają:
1 - prawda w sensie bezwzględnym (prawda absolutna)
0 - fałsz w sensie bezwzględnym (fałsz absolutny)
B.
Jeśli jedynki i zera w równaniu algebry Boole’a (sic!) prof. Newelskiego nie znaczą tego co wyżej, to co one oznaczają?
Czyli:
Jaka jest jeszcze inna interpretacja zer i jedynek w logice ziemian?
Czy może odpowiedzieć na te dwa, historyczne i absolutnie kluczowe pytania?
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Komandor
Gość
|
 Wysłany: Pią 15:41, 01 Kwi 2016 Temat postu: Wysłany: Pią 15:41, 01 Kwi 2016 Temat postu: |
|
|
|
A gdzie ten cytat?
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pią 15:46, 01 Kwi 2016 Temat postu: Wysłany: Pią 15:46, 01 Kwi 2016 Temat postu: |
|
|
| Komandor napisał: | | A gdzie ten cytat? |
Chodzi ci o prof. Newelskiego?
Dzięki któremu dorwałem się do logiki matematycznej ziemian udowadniając jej wewnętrzną sprzeczność czysto matematyczną?
Tu, niżej:
| fiklit napisał: | | Wydumane to strasznie. |
Pozwolisz że na początek zacznę rzeczowo i absolutnie bez żadnego wydumania, po prostu zacytuję prof. Newelskiego (Uwaga 2.7):
[link widoczny dla zalogowanych]
Pani w przedszkolu do 5-cio latków:
A.
Jutro pójdziemy do kina lub do teatru
Y=K+T
Zbudujmy tabelę prawdy dla tego zdania:
| Kod: |
Tabela prawdy dla zdania Y=K+T
K T Y=K+T
A: 1 1 =1
B: 1 0 =1
C: 0 1 =1
D: 0 0 =0
|
Równanie algebry Boole’a (sic!) prof. Newelskiego, czyli spis z natury (piszę to co widzę) w naturalnej logice matematycznej człowieka.
Cytuję prof. Newelskiego:
Z tabelki tej odczytujemy, że funkcja logiczna Y jest prawdziwa wtedy i tylko wtedy, gdy:
1.
1ABC: Y=1 <=> A: K=1 i T=1 lub B: K=1 i T=0 lub K=0 i T=1
Czy możesz odpowiedzieć na proste pytania?
1.
Czym są symbole K, T oraz Y w nagłówku powyższej tabeli?
Możliwości masz wyłącznie dwie:
A.
To są zmienne binarne których wartości logicznej w dniu dzisiejszym (w chwili wypowiadania zdania Y=K+T) nie znamy
B.
To są stałe symboliczne których wartość logiczna jest znana i której to wartości logicznej nie jesteśmy w stanie zmienić
2.
Czym są zera i jedynki w równaniu algebry Boole’a (sic!) prof. Newelskiego?
1ABC: Y=1 <=> A: K=1 i T=1 lub B: K=1 i T=0 lub K=0 i T=1
A.
W szczególności czy te jedynki i zera oznaczają:
1 - prawda w sensie bezwzględnym (prawda absolutna)
0 - fałsz w sensie bezwzględnym (fałsz absolutny)
B.
Jeśli jedynki i zera w równaniu algebry Boole’a (sic!) prof. Newelskiego nie znaczą tego co wyżej, to co one oznaczają?
Czyli:
Jaka jest jeszcze inna interpretacja zer i jedynek w logice ziemian?
Czy może odpowiedzieć na te dwa, historyczne i absolutnie kluczowe pytania?
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Gość
|
 Wysłany: Pią 15:49, 01 Kwi 2016 Temat postu: Wysłany: Pią 15:49, 01 Kwi 2016 Temat postu: |
|
|
| rafal3006 napisał: | Czym są zera i jedynki w równaniu algebry Boole’a (sic!) prof. Newelskiego?
A.
W szczególności czy te jedynki i zera oznaczają:
1 - prawda w sensie bezwzględnym (prawda absolutna)
0 - fałsz w sensie bezwzględnym (fałsz absolutny)
B.
Jeśli jedynki i zera w równaniu algebry Boole’a (sic!) prof. Newelskiego nie znaczą tego co wyżej, to co one oznaczają? |
Jedynka (1) pisana odręcznie powstała z rozpadu Zera (0).
To bardzo łatwo sobie wyobrazić:
- począwszy od dolnej prawej części zera utwierdził się ogonek jedynki, a część prawa zera nadłamała się i obwisla. Reszta zera wyparowała, albo rozsypała się w drobny mak.
Wszystkie inne cyfry powstały podobnie z zera. Ósemka to zero skręcone ze złości. Trójka powstała przez wyschniecie dwóch cząstek zera, a dwójka wywinęła się do góry i przekręciła z nad górnej części zera.
Nawet czwórka powstała z zera; tylko nie taka czwórka jak drukowana.
To wszystko wymyśliłem Ja i jest to odkrycie na miarę przyszłości.
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pią 15:56, 01 Kwi 2016 Temat postu: Wysłany: Pią 15:56, 01 Kwi 2016 Temat postu: |
|
|
Kubuś już obalił logikę matematyczną ziemian udowadniając jej wewnętrzną sprzeczność - nasza Krowa obali wszystko pozostałe, znaczy wszystko co się rusza 
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
rafal3006
Opiekun Forum Kubusia
Dołączył: 30 Kwi 2006
Posty: 39799
Przeczytał: 12 tematów
Skąd: z innego Wszechświata
Płeć: Mężczyzna
|
 Wysłany: Pią 15:56, 01 Kwi 2016 Temat postu: Wysłany: Pią 15:56, 01 Kwi 2016 Temat postu: |
|
|
Kubuś już obalił logikę matematyczną ziemian udowadniając jej wewnętrzną sprzeczność - nasza Krowa obali wszystko pozostałe, znaczy wszystko co się rusza 
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
hushek
Bloger na Kretowisku
Dołączył: 23 Lut 2011
Posty: 6781
Przeczytał: 0 tematów
Skąd: umiłowany kraj
Płeć: Mężczyzna
|
 Wysłany: Pią 17:26, 01 Kwi 2016 Temat postu: Wysłany: Pią 17:26, 01 Kwi 2016 Temat postu: |
|
|
| Komandor napisał: | (...)
Ja na własne oczy widziałem jak ludzie w zgodzie ze smokami współżyli. Dokładnie Wikingowie.
Gupi ten Maniek i na dodatek nie obyty ani kulturalnie ani naukowo...
A pochowanie smoków? No cóż... jak współżyli to pewnie chowali. |
Ale kąkrętnie to o jakich Wikingów sjem roshodzi ?
Bo to jednak różnica pewna jest.
Wef serialach szwedzkich to majom - te Wikongi zenby popsute, a znowusz w tych amerykańskich produkcjach popylają se f najlepsze w kreacjach od Gucciego jakiegoś , czy jak mu tam lup innego modnego miglanca typu Dżender i muwio se - Haj,...na pszywitanie....oras - hałdujudu ?
A pachno pszy tem co najmniej Farenhaitem...i to nje podrubom jakomś - made in z bazarku dzielnicowego.
Tak, czy owak ze smokami nie współżyjom zusammen do kupy na taśmie filmowej, bo to nieporawne jest politycznie.... zaruwno po tej, jak i po tamtej stronie Wielgiej Wody.
Co innego Krak unt Jego załoga co to Mniemców nje chcieli. O te ludzie słusznego pochodzenia som - take słowiańskie, no rze ja pierdole, płci obojga zreszto - ze smokamy - jak najbardziej...
Taksze cuś pierdolisz Komandorze, njematotamto...
cbdu... 
Nic podejścia nałókowego, no kurwa nic... 
Ostatnio zmieniony przez hushek dnia Pią 17:29, 01 Kwi 2016, w całości zmieniany 1 raz
|
|
| Powrót do góry |
|
 |
| Zobacz poprzedni temat :: Zobacz następny temat |
| Autor |
Wiadomość |
Komandor
Gość
|
 Wysłany: Pią 19:29, 01 Kwi 2016 Temat postu: Wysłany: Pią 19:29, 01 Kwi 2016 Temat postu: |
|
|
No Wiślanie ze smokami a jak! Normalka. Ale za to te ze wsi Warszawa bajdy opowiadają te Mazury niemożebne, że z syrenkami cośtam cośtam...
To już całkiem nienaukowe, oj nie, bo jak z taką syrenką można cośtam cośtam jak ona podejścia przez ogon całkiem nie ma...? A?
No co gupi Mańku?
|
|
| Powrót do góry |
|
 |
|
|
Nie możesz pisać nowych tematów
Nie możesz odpowiadać w tematach
Nie możesz zmieniać swoich postów
Nie możesz usuwać swoich postów
Nie możesz głosować w ankietach
|
fora.pl - załóż własne forum dyskusyjne za darmo
Powered by phpBB © 2001, 2005 phpBB Group
|


















